深度学习(DL)的能量需求特性引起了对神经形态架构的极大关注，因为它们能够以非常低的能耗在非常高的频率下运行。为此，神经形态光子学是最有前途的研究方向之一，因为它们能够达到每MAC飞焦耳的效率。虽然电光物质为深度学习提供了一个快速高效的平台，但它们也引入了各种影响有效位分辨率的噪声源，给深度学习量化带来了新的挑战。在这项工作中，我们提出了一种量化感知的训练方法，该方法以混合精度的方式逐步对层进行比特缩减，使我们能够在部署时运行低精度的网络，并进一步提高所开发的加速器的计算率，同时保持低能耗。利用中间层精度要求较低的观察结果，我们提出通过正态分布每层的降维概率来逐步降低层的比特分辨率。实验证明了混合精度量化在性能和推理时间上的优势。此外，我们在不同的任务、架构和光子配置中对所提出的方法进行了实验评估，突出了其降低DL模型平均位分辨率的巨大能力，同时显著优于评估的基线。

　　深度学习(DL)是发展最快的领域之一，主导并显著加速了工业发展和学术研究的不同方面的进步[1]。生成式预训练转换器3 (GPT-3)[2]最近引起了极大的关注，是DL在复杂任务(如自然语言处理)中日益成功应用的最新成果之一。在人工生成图像方面也取得了类似的成就，如DALL-E[3]，具有类似变形金刚架构的计算机视觉[4]，以及在玩超人级别的游戏方面，如AlphaZero[5]。

　　为此，神经形态光子学是最有前途的方法之一，最近的布局已经为每MAC效率飞焦耳铺平了现实的路线图[6]，可能允许人们以非常低的能量消耗(焦耳)执行MAC操作。这些结构能够传输接近光速的光信号——显著超过它们的电子对应体——然后操纵它们来提供神经元的功能[7,8]。为此提出了几种方法，既采用纯光学器件[9]，也采用先进的高速光电物质[10,11]。这种架构提供了超高的计算速率，因为它们在非常高的频率下运行，利用了它们巨大的带宽带来的巨大并行能力[12,13,14]。最重要的是，它们在非常低能量和功耗的信封中运行[15]，这使得它们在DL应用中具有吸引力，特别是在需要高频和低能耗的应用中，例如光纤网络通信[16]和网络监控[17,18]。

　　虽然电光物质为深度学习提供了一个快速高效的平台，但它们也引入了各种影响有效位分辨率的噪声源。更具体地说，光子计算包括使用数模(DAC)和模数(ADC)转换，以及参数编码、放大和处理设备，如调制器、光电二极管(pd)和放大器，这些设备不可避免地会在推理过程中引入模拟精度的降低，因为每个组成部分都会引入影响电光链路位分辨率特性的相关噪声源。因此，当应用较高的线路速率时，引入的噪声增加，转化为较低的比特分辨率。基于神经网络可以在推理过程中补偿噪声这一事实，为此已经提出了几种增强方法[19,20]。这些方法的范围从考虑光学神经元的有限带宽[21,22]，使用高斯白噪声模拟噪声[23]到更高级的方案，例如初始化考虑噪声和数据分布的网络[24]。此外，现有方法通过应用后量化[25]或量化感知训练[26,27]技术来处理由有限精度物质和AD/DA转换引起的噪声损伤，从而显著提高了模型的性能[28]。

　　通常，模拟精度的退化可以通过量化过程来模拟，通过将连续信号的连续集映射到有限的离散值集，将连续信号转换为离散信号[29]。这可以通过舍入和截断输入信号的值来实现。尽管量化技术在深度学习领域得到了广泛的研究[30,31,32]，但它们通常针对的是包含大量剩余参数但对模型整体性能贡献较小的大型卷积神经网络(cnn)[33,34]。这些大型架构很容易被压缩，相比之下，较小的网络，如目前为神经形态光子学开发的网络，其中每个参数对模型的最终输出都有很大贡献[30]。此外，现有的研究主要集中在忽略输入和偏差的部分量化模型上[30,35]。当使用高斜率光子激活时，这些限制会进一步被夸大，这就要求采用考虑实际物理实现的不同训练范式[36]。事实上，神经形态光子学对DL模型的量化提出了新的挑战，需要对现有方法进行适当的调整，以适应光子衬底的独特局限性，例如使用光子激活函数。此外，神经形态光子学中应用的量化方案通常遵循非常简单的均匀量化，因为它依赖于DAC/ADC模块对信号进行均匀对称量化[37,38]。这与传统上用于深度学习模型的可训练量化方案[39]以及混合精度量化[40,41]的方法不同。

　　图1

　　

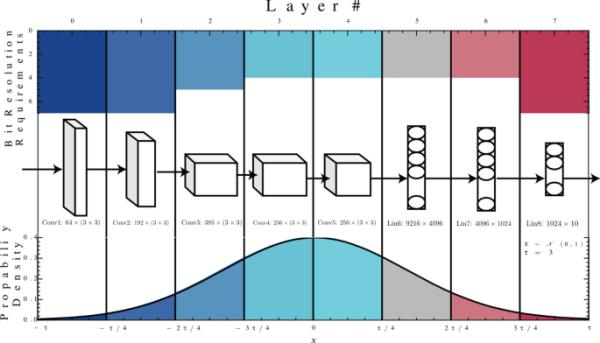
　　描述了基于已进行的实验(第4.1节)的AlexNet8的每个层的比特要求。正态分布可以用来表示混合精度方案中逐层比特分辨率降低的概率

　　在部署期间能够在低精度网络中运行，可以通过提高所开发的加速器的计算速率，同时保持较低的能耗，进一步提高模拟计算的潜在用途[42,43]。在这项工作中，我们关注最近提出的高速模拟光子计算[44]，它解锁了光子神经网络(PNNs)的动态精度能力[45,46]。我们提出了一种随机混合精度量化感知训练方案，该方案能够基于观察到的应用架构和配置的比特分辨率分布，以混合精度的方式调整层之间的比特分辨率。更具体地说，它逐渐降低层的比特分辨率，将较低比特分辨率的概率附加到中间层而不是外层，遵循正态分布，利用并评估了中间层比特精度可以显着降低而不会对模型性能产生负面影响的观察结果，同时显着减少了推理时间[45]。提出的量化感知训练方法考虑了可学习参数、输入和激活值的均匀量化所产生的量化噪声，同时根据它们的位置和训练历元逐渐降低比特分辨率。我们声称网络中比特分辨率的分布形状是倒钟形，因此，我们提出了一个正态分布概率来降低比特分辨率，如图1所示。

　　所提出的方法使我们能够以渐进和混合精度的方式降低模型的平均比特分辨率，而不会显著降低性能。因此，它为我们提供了探索和应用低精度配置的能力，与固定精度模型相比，提高了计算速度。为了证明所提出方法的有效性，我们将其应用于各种应用的广泛架构中，从图像分类到使用光子激活函数的金融时间序列预测。基于[44]中提出的光子架构，我们采用了[45]中提出的框架来定量评估低比特精度模型的推理时间，从而突出了应用所提出的混合精度量化感知训练方法的好处。本文是我们在[26]中提出的初步工作的扩展版本，其中提出了一种面向pnn的量化感知训练方法，该方法考虑了均匀量化引入的量化噪声。在这项工作中，我们进一步扩展了我们之前的工作，提出了一种混合精度方法，在量化感知训练过程中逐渐降低层的比特分辨率，同时考虑到它们在人工神经网络(ANN)和训练时代中的相对位置。

　　本文的其余部分结构如下。第2节提供了光子DL的必要背景，而提出的方法在第3节中进行了介绍和描述。最后，在第4节给出实验评价，在第5节得出结论

　　与软件实现的人工神经网络类似，光子人工神经网络基于感知机，其最终目标是逼近函数。更精确地说，光子神经网络的输入信号表示为，其中表示第-层输入特征的个数。训练数据集中的每个样本都用一个向量来标记，如果是分类任务(C表示类的数量)，则第-个元素等于1，其他元素为0;如果是回归任务(C表示回归目标的数量)，则为连续向量。mlp通过使用多个层进行近似，即学习由权重和偏差组成的参数。随后，将每层的输出记为:

　　（1)

　　神经元线性部分的输出被馈送给一个非线性函数，称为激活函数，形成该层的最终输出:

　　（2）

　　人工神经网络的训练是通过更新其参数来实现的，使用反向传播算法，旨在最小化损失函数，其中表示训练标签和网络的输出。交叉熵损失常用于多类分类情况:

　　（3）

　　除了前馈神经网络，在本文中，我们还将量化方法应用于简单应用的递归神经形态光子结构[47,48]。应用的循环架构受益于现有的光子前馈实现[49]，同时使用反馈回路。根据上述符号和循环架构接受序列数据作为输入的事实，设为多维时间序列，而设表示在第t个时间步输入的观测值。然后，使用输入权值对输入信号进行第i个神经元的加权。此外，将递归神经元在前一个时间步长的输出对应的递归反馈信号记为，也用递归权值进行加权。第i个循环神经元的最终加权输出计算为:

　　（4)

　　应该注意的是，我们省略了偏置项以简化所使用的符号。然后，将该加权输出馈送到所使用的光子非线性中，得到神经元的最终激活为:

　　(5)

　　在这种情况下，研究使用了两个光子激活函数。首先，定义光子s型激活函数[50]:

　　（6）

　　其中参数和被调优以适应在真实硬件设备上实现的实验观察结果[50]。

　　并将光子正弦激活函数应用于实验测试评价。光子布局对应于采用马赫-曾德尔调制器器件(MZM)[51]，该器件与PD[52]一起将数据转换为光信号。该光子激活函数的公式为:

　　(7)

　　值得注意的是，由于这些光子激活的输入域范围很窄，训练更加困难，因为网络容易饱和，导致收敛速度较慢，甚至停止训练。

　　图2

　　

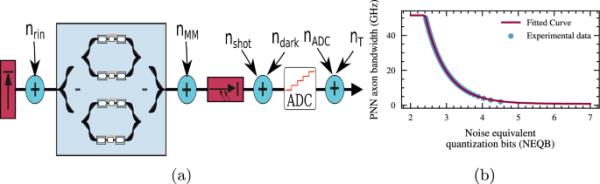
　　a PNN噪声源分解，b PNN轴突带宽与等效比特分辨率

　　为了评估所提出的方法，我们使用了[45]中提出的一种新的分析框架，该框架能够将底层光子元件的可用光电带宽与PNN的相应等效位分辨率相关联。通过这种方式，我们能够确定定义PNN的计算速率和可实现的位分辨率之间关系的主要物理机制。反过来，这揭示了遵循电子人工神经网络加速器范式的高速pnn的延迟-精度权衡[53,54]。图2a描述了影响PNN位分辨率性能的噪声源的原理图分解，即*********与激光源的噪声贡献相关，对应于光子矩阵乘法电路引入的噪声，对应于光电二极管电流的随机波动，对应于光电二极管的有限暗电流，与所使用的ADC施加的量化噪声相对应，最后与PNN的热噪声相关。利用上述框架，在典型的插入损耗为30dB的神经形态光子布局范围内，当参考激光发射功率为16dBm时，可以近似于大规模PNN部署的特性，并考虑矩阵噪声的归一化标准差等于，剩余噪声源等于[45]中提出的标准化值，我们在图2b中给出了PNN轴突上可实现的有效比特数与带宽之间的关系。

　　在这项工作中，我们通过提取所需的乘法累积操作(mac)的数量，定量地评估了所提出的方法在推理时间上的性能。推理时间是根据每层的比特分辨率和百万次乘法累加运算(mmac)来计算的。为了根据噪声等效比特来计算每个PNN轴突的带宽，我们对[45]测量[44]的PNN配置的实验数据拟合一个指数函数，其公式为:

　　（8)

　　式中，和为系数和。我们根据硬件规格限制最大可用带宽。模型的最终执行时间(秒)计算为:

　　（9）

　　其中，和分别为-层的mmac数和等效位分辨率。

　　在这项工作中，我们提出了一个量化感知训练框架，该框架考虑到网络层的位置和训练纪元，逐渐降低网络层的比特分辨率。所提出的框架面向pnn，更具体地说，面向最近提出的动态精度体系结构[44]，但也可以用于其他神经形态体系结构，而不会失去通用性。

　　所提出的量化感知训练框架考虑了由有限精度模块引起的量化误差。量化感知方案利用人工神经网络在第一次训练时补偿已知噪声源的固有能力[24]。更具体地说，通过对前向传递过程中涉及的所有参数进行均匀量化，网络使用量化参数进行训练，因此量化误差累积并通过网络传播到输出并影响所使用的损失函数。通过这种方式，网络可以适应较低精度的信号，使其在推理过程中对降低的比特分辨率具有更强的鲁棒性，显著提高了模型性能。在本文提出的混合精度量化感知训练框架中，受到[28]中量化方案的启发和扩展，第-层响应中涉及的每个信号首先在特定的浮动范围内量化。然后，在网络前向传递过程中，注入量化误差来模拟量化过程中舍入的影响，而在反向传播过程中，忽略舍入并使用恒等函数进行近似。通过这种方式，反向传播过程可以在不改变现有训练管道的情况下进行，因为在训练过程中输入、权值、模型参数和激活值都以浮点格式存储。因此，我们提出的方法属于所谓的直思维估计器(STE)量化族[41]。

　　更具体地说，每个涉及的信号首先映射到相应的量化码仓，基于所使用的位分辨率，并假设每个码仓具有相同的长度。因此，假设表示信号的某个值，例如输入、权值或输出，则应用量化函数可得到信号的量化版本为:

　　（10)

　　式中为特定信号的比例因子，为零点，表示-位正整数的取值范围，即和，而剪辑函数定义为:

　　(11)

　　比例值计算为:

　　（12）

　　和表示信号的代理最大值和最小值。然后，计算零点:

　　（13）

　　然后，我们可以使用反量化函数将值转换回其浮点表示形式:

　　（14）

　　根据上述符号，在应用激活函数之前，网络第-层的量化响应可计算为

　　(15）

　　其中表示量化过程，然后是向量的去量化，可以在向量上应用元素，而和表示第-层的量化权重和偏差。最后，输出通过神经元的光子激活函数:

　　(16)

　　图3

　　

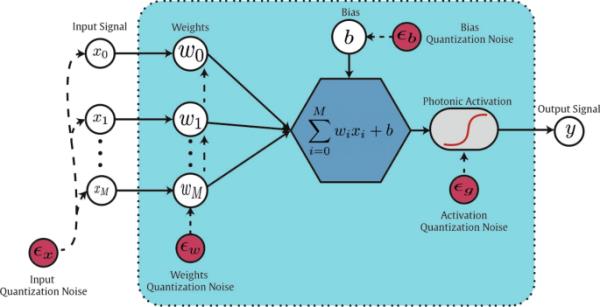
　　图中为前向传递过程中注入量化噪声的线性神经元

　　因此，所有参与神经元输出的信号都分布在和之间的一个均匀的浮动范围内，并且可以用比特表示。因此，在训练过程中，量化误差作为噪声信号在网络中传播。这可以通过在前传过程中注入量化误差来实现，如下所示:

　　（17)

　　其中，和分别是权重、线性响应和激活量化误差，它们是用该函数得到的原始值与量化值之差计算得到的。例如，对于权重，量化误差计算为。前馈网络的这一过程如图3所示。值得注意的是，在不损失通用性的情况下，相同的量化框架也可以应用于其他体系结构，例如循环体系结构。需要注意的是，在训练过程中，量化效果是模拟的，而反向传播的过程和往常一样，也就是根据传播的损失对原始参数进行更新。

　　一个信号的代理最小()和最大()值，其中均匀桶的规模取决于，可以显著影响量化噪声，无论是在训练和推理。较大的for值(或较小的for值)源于信号的异常值，导致很大一部分信号值落在相同的桶中，从而导致信息丢失和高量化噪声。为此，我们提出了一种利用指数移动平均线(EMA)在训练过程中调整和值的方法。EMA能够消除向量和矩阵中的异常值，以这种方式平滑量化感知训练过程。因此，模型在训练过程中对异常值具有更强的鲁棒性，反过来，在推理过程中对注入信号的量化噪声具有更强的鲁棒性。

　　由于在训练过程中变换了每个信号的分布，因此在每个训练迭代中迭代地应用EMA。为此，在每次训练迭代中计算信号的代理最小()和最大值()值为:

　　(18) (19)

　　其中为EMA的权重参数，更新应用于。

　　除了量化感知训练外，我们还提出了一种渐进的方法，根据层的位置和训练历元来降低层的位分辨率。该方法考虑了网络各层比特需求的预期或观测分布，并在训练过程中以混合精度的方式降低其比特分辨率。更准确地说，在这项工作中，我们声称中间层需要较低的比特分辨率，而不是第一层和最后一层，当应用较低的比特分辨率时，中间层容易受到量化噪声的影响，并对模型的性能产生负面影响。对于第一层，我们认为根据数据处理不等式，一层丢失的信息在后续的层中无法恢复[55]。在另一端，网络的最后一层专门用于将提取的特征投影到影响模型预测的多维输出空间。在训练过程中，特别是当使用交叉熵损失函数时，相似的样本(例如，MNIST数据集中的数字2和5)被放置在超空间的附近，而明显不同的样本被放置在远离另一个的位置(例如，MNIST数据集中的数字1和5)。因此，当应用到最后一层时，模型更容易受到噪声的影响，特别是当类似的样本被包括到评估数据集中时，以这种方式降低了它们的性能。

　　为此，我们在训练过程中为中间层附加更高的比特分辨率降低概率，而对于外层，我们附加较小的概率。概率根据高斯分布分布到各层，并且在每个历元中，概率根据引入的超参数增加。从概念上讲，所提出的方法的动机是遗传算法(GAs)中广泛使用的轮盘赌选择方法[56]。与基于适应度值为染色体附加静态概率的遗传算法不同，该方法根据层的位置将概率附加到正态分布的层上，并在训练过程中逐渐增加概率。

　　图4

　　

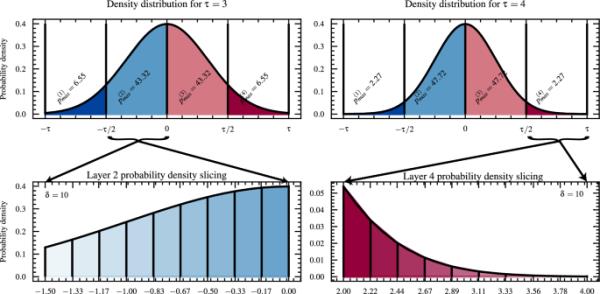
　　在图的上一行，给出了不同超参数值的最大概率密度。在第二行中，根据每列的超参数给出了第2层和第3层的切片最大概率密度。每层最大密度的切片数取决于超参数。这些层从不透明度较低的切片开始到不透明度较高的切片，以这种方式表示概率增量

　　更准确地说，对于每一层，我们定义降低其位分辨率的最大概率。如果一层达到最高概率，则概率保持不变，直到训练结束或直到发生位减少。如果在第-th epoch执行位缩减，则在下一个epoch将从最小概率开始。更具体地说，在每个时代，我们从各自的高斯分布中绘制这样的值作为层数，其中表示层数，并分别定义高斯分布的平均值和标准差，它们是所提出方法的超参数。每一层都被赋予最大降低其位分辨率的概率，这取决于层的位置，用标准正态分布的累积分布函数(CDF)可以计算为:

　　（20）

　　给出位于和之间范围内的概率密度，其中定义为表示高斯分布的均匀切片，如图4顶部所示。表示切片的宽度，影响每层的最大概率。例如，通过增加，内层的最大概率增加，同时减少外层的概率。当值减小时，内层的最大概率减小，外层的最大概率增大。

　　为此，如果层在其最大概率上，则混合精度算法检查从各自的高斯分布中提取的点是否在范围内，概率在-时间步长。如果和，其中定义了允许的最小位分辨率，则-层的位分辨率下降到，其中定义了位减少步骤。这可以表示为:

　　（21）

　　基于理论和实验观察[41]，我们引入了一种随机方法，该方法以系统的方式提供了更大的可能性，在不严重影响网络性能的层中减少比特，我们还在量化感知训练期间引入了一种渐进的方法。在层中给出完整的范围来降低它们的位分辨率，因此，每个历元的最大可能性，这将导致在训练的最初几个历元的精度非常低。因此，在训练的第一阶段，网络不稳定且不接近其收敛阶段，量化噪声会非常高，给训练带来困难，如梯度消失现象[57]。这可能导致不良的局部最小值和显著的性能下降。为此，我们提出了一种渐进的比特减少方法，该方法在每个历元中增加层的概率以降低其分辨率。这是通过重新均匀切片层的最大可能范围来实现的，如图4第二行所示。

　　更具体地说，我们引入一个除数值，它将均匀切片中的最大可用范围划分为:

　　其中称为第-层的活动范围。

　　在每个历元，活动范围要么增加，直到它的最大可用范围，相当于第-层的最大概率密度，或者直到从各自的高斯分布中得出的点下降到活动范围内。定义了从训练开始或从最后一个位缩减开始的历元。因此，在绘制的值不在活动范围内的每个训练历元，，如果不等于，则增加一个单位，以这种方式将活动范围增加一个切片，表示为

　　(22)

　　这两种情况定义了正态分布两侧的概率增加，如图4第二行所示。如果层的范围在分布的负侧，那么通过解锁右侧的下一个切片来增加概率。否则，如果层位于分布的正侧，则通过降低下界来解锁另一个切片来增加概率。在这两种情况下，第i层执行位减少的概率都增加了。在这种情况下，活动范围被重置为最小值，并且该方法根据进行位缩减。这个过程使我们能够平稳地增加注入的量化噪声，同时确保噪声首先被引入到对其影响更鲁棒的层中。第-层在第-次epoch将其精度降低比特的概率为:

　　（23）

　　其中在每个历元计算为:

　　（24）

　　与。

　　在这项工作中，我们对所有实验评估案例使用默认的超参数值。更具体地说，我们经验地建议在设置时使用均值为0，方差为1的正态分布。每一层比特减少的概率逐渐增加取决于，反过来，我们设为，其中为epoch的个数。最后，将位元缩减步骤设置为。应该提到的是，为了简单起见，所提出的方法是针对偶数层提出的，但它可以直接用于奇数层，只需将正态分布向左或向右移动。

　　

　　

　　在算法1和算法2中提出了该框架。算法1是混合精度量化感知训练，算法2是参数向量或矩阵的量化。更具体地说，算法1将epoch的个数、每层的可训练参数(即权重和偏置)、初始和最小位分辨率以及混合精度量化感知训练的超参数，如、和作为输入。首先，该算法正确构建用于每层(第2行)的最大概率的切片，并将最小活动概率(第4-5行)和初始比特分辨率(第6行)附加到它们上。然后，网络以量化感知的方式(第7-21行)进行训练，通过量化前向传递(第8-19行)期间涉及的每个参数，应用所提出的渐进比特缩减方法，计算第- epoch的比特分辨率。每一层(第8-15行)。首先，提出的方法从各自的高斯分布(第9行)为每一层绘制一个值，并检查它是否在该层的活动范围内(第10-15行)。如果在活动范围内(第10-12行)，则必要时降低位分辨率(第11行)，然后将活动概率重置为最小值(第12行)。如果随机值不在活动范围内(第13-15行)，则活动概率增加，这取决于是否存在它们的最大概率。

　　之后，量化感知训练可以照常进行。算法2中解释的参数量化应用于:(第-层的权重)、(层的偏差)和(层的输入)，然后应用于前向传递期间每层的输出。然后，反向传播通过应用损失函数来更新原始权重和偏差。更具体地说，在算法2中，给出了矩阵或矢量参数的量化。最初，我们计算和使用EMA(第2-3行)，它用于计算规模和零点(第4-5行)。反过来，在(第6行)和返回到浮点范围(第7行)之间的一组有限整数中被量化，这是算法的最终输出。

　　相关的内容

　　摘要

　　1 介绍

　　2 背景

　　3.提出了f

　　ramework

　　4 实验e

　　估值

　　5 结论

　　数据可用性

　　参考文献

　　致谢

　　作者信息

　　相关的内容

　　搜索

　　导航

　　#####

　　为了证明所提出方法的有效性，我们首先进行实验，根据每一层的位置研究其比特需求，结果表明，与外层相比，中间层需要更低的比特分辨率。反过来，我们给出了实验评估结果，显示了应用混合精度量化技术的巨大推理时间优势。之后，我们通过将其应用于不同的神经网络架构和配置来评估所提出的方法，包括多层感知器(mlp)， cnn和递归神经网络(rnn)。对于所有应用的架构，我们使用两种不同的光子配置来评估所提出方法的性能，基于光子s型和正弦激活函数，见第2节。更具体地说，我们在两个图像分类任务中展示了它的能力，使用MNIST和CIFAR10数据集，以及在高频金融时间序列预测中，使用FI2010数据集[58]。我们报告了在多次评估运行中获得的平均位分辨率范围为2到7位的实验结果。最后，在CIFAR10任务的情况下，我们应用第2节介绍的评估框架，在推理时间方面证明了所提出方法的效率。对于基准测试，我们使用两个统一的量化基线，(a)训练后量化方法，使用矩阵的最小值和最大值来均匀分布不同的值，(b)量化感知训练方法，在第3节中提出，在训练期间使用EMA来计算代理的最小值和最大值。

　　图5

　　

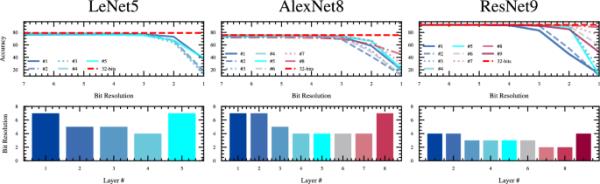
　　图中描述了3种不同卷积架构下的混合精度需求。最上面一行给出了每一层的精度和位分辨率之间的关系。在最下面一行，我们绘制了没有显著精度下降的最小位需求()

　　我们通过实验证明了每层的比特需求，通过研究三种著名的卷积架构中不同的比特分辨率配置。更具体地说，我们将LeNet5 [59]， AlexNet8[60]和ResNet9[61]应用于传统的CIFAR10图像分类任务，并使用AdamW[62]优化器进行100次epoch的训练，学习率为0.001，权重衰减值为。在为每个不同的架构编译了5次训练运行后，我们在不同的比特分辨率上对它们进行评估，开始从第一层到最后一层使用它们，应用最简单的训练后量化方法。量化方法分别使用最小值和最大值对参数进行统一量化。我们提出了在2到7位之间的每个位分辨率的5次评估运行的平均精度，应用于网络的每一层。这允许我们研究每层的位分辨率和模型的整体性能之间的关系。

　　实验结果如图5所示。更具体地说，在上行中，我们绘制了应用于不同层时不同位分辨率的平均评估精度。当我们使用标准的32位浮点运算时，红色虚线表示超过5次计算运行的平均精度。不同的线表示模型的不同层。在底部一行中，我们报告了每层的最小位分辨率要求，而精度没有明显下降。在不可能达到可接受精度的情况下，我们报告最大可用位分辨率，这是7位。我们应该注意到，我们的分析没有考虑到位需求的内部依赖关系，这意味着当前一层也降低了位分辨率时，对一层的位分辨率的影响，因为我们一次只对一层应用位降低。

　　在图的第一行中，我们可以看出，网络的第一层和最后一层要么从比中间层更低的性能开始，要么在更低的比特减少下，它们的性能也显著下降。例如，LeNet5和AlexNet8的最后一层被描述为即使在大于3的位分辨率下也能实现较低的精度。我们在ResNet9架构中也观察到类似的行为，即使在应用3位分辨率时，最后一层的性能下降也是可见的。在相同的体系结构中，当我们在模型的第一层应用较低的位分辨率时，性能也会崩溃。更准确地说，当将位分辨率从8位降低到3位时，会发生接近于。

　　图的第二行清楚地描述了所有三种架构所遵循的等效行为，其中我们报告了在没有显着性能下降的情况下每层的最小位分辨率要求。我们观察到，当我们对LeNet5和AlexNet8架构的第一层和最后一层应用比特缩减时，它们无法补偿等效噪声并抵抗性能下降。因此，这些层的最小位分辨率是可用的最大值，即7位。在ResNet9架构中也观察到类似的行为。尽管由比特减少引起的量化噪声可以通过第一层和最后层大于4位的比特分辨率进行补偿，但它们仍然无法调整到中间层能够达到的较低的比特分辨率，例如2位和3位。我们将这种行为归因于这些层对网络最终输出的贡献的重要性。一方面，网络的第一层负责构建下一层用来对样本进行分类的表示图，因此，根据数据处理不等式[55]，当向其中注入量化噪声时，例如在考虑图5的前两层中，会导致严重的信息丢失，而这些信息在后续层中无法恢复。因此，提取的特征图缺乏重要的细节，这些细节可能会从网络的后续层中使用，以正确分类样本。另一方面，最后一层本质上容易受到噪声的影响，因为模型传统上是用交叉熵损失训练的，这通常会导致分类神经元，即分类层的神经元，根据样本相似度，相对于错误的分类样本，正确的分类样本输出相对较大的值[63]。这样，在没有正则化或标签平滑技术的情况下，输出不是根据其类别分布在等距聚类中，而是以更线性的方式分布，使它们容易受到噪声现象的影响，例如量化噪声[46]。值得注意的是，在训练过程中不考虑噪声会导致显著的性能下降，而考虑噪声可以避免这种下降[24,28]，下面的实验结果也证明了这一点。

　　图6

　　

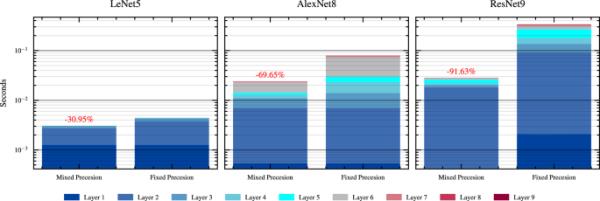
　　描述了应用于不同体系结构的混合和固定精度量化方法的推理时间。推理时间轴(y轴)是对数刻度和秒单位。在混合精度条的上方，报告了应用混合精度量化获得的推理时间减少百分比

　　为了证明混合精度方法在推理时间方面的有效性，我们在图6中绘制了依赖于每层的NEQB的预期推理时间，应用了第2节中提出的分析框架。更具体地说，对于每种体系结构，左栏表示应用混合精度量化技术所需的推理时间。其层的比特分辨率由之前的实验评估得到，如图5第二行所示，定义了混合精度训练后量化技术的理想情况。在右栏中，报告了固定精度的量化，其中每层的分辨率为7位。即使在较小的模型中，推理时间的减少也令人印象深刻。例如，在LeNet5架构中，模型的推理时间比固定精度时间降低了1/3。虽然模型的大小增加了，因此每层的mac增加了，但推理时间进一步减少了，正如ResNet9架构所描述的那样，在ResNet9架构中实现了90%的减少。这是一种预期的行为，因为较大的模型是过度参数化的，每层有大量的mac，因此与较小的模型相比，每个参数对最终输出的贡献较小。为此，可以在不显著降低性能的情况下，对网络采用较小的位分辨率，如图5所示。这与推理时间相对于比特分辨率呈指数级减少的事实相结合，如图2节中的图2b所示，我们观察到在时间性能方面的巨大改进。

　　对于图像分类基准，我们使用两个传统数据集，MNIST和CIFAR10，分别应用两种架构，一个4层MLP和一个8层CNN。小型架构用于演示该方法在架构上执行的能力，这些架构可以基于当前的能力和限制，使用光电组件潜在地实现。对于MNIST案例，所采用的架构由4个线性层组成，第一层和最后一层各有10个神经元，中间层有20个神经元。在每个隐藏层之后应用光子激活函数。在CIFAR10的情况下，我们使用使用残差连接的8层CNN。更具体地说，CNN由3个卷积层、2个残差块(残差块各由2个卷积层组成)和一个输出分类层组成。前两个卷积层都使用内核，没有偏差，分别使用64和128通道，应用等于1的stride和padding。这两层后面都有一个批处理规范化层，而第二层后面也有一个maxpooling层，内核大小和步长等于2。maxpooling层的输出随后被传递给残差块，残差块由两个卷积层组成，这两个卷积层后面都有一个批处理归一化层，其中残差块的输入被添加到其输出中。在第五层卷积层之后和输出线性层之前应用类似的256通道残差块。CNN架构是一个类似但更小的ResNet架构，名为ResNet8。

　　对于这两个图像分类任务，我们使用RMSProp优化器，学习率等于0.0001，批大小等于256。我们训练了100个epoch的模型，并重复该过程5次，以报告表1和表2中每种评估方法的评估精度的平均值和方差。对于所提出的方法，我们报告了平均位分辨率的平均评估精度，其中后者是通过对层的位分辨率进行舍入来计算的。我们使用所提出方法的默认超参数将初始位分辨率设置在8到3位之间。作为参考，我们还报告了32位全精度模型在5次运行中的平均评估精度。

　　表1 e在MNIST数据集上使用完全co来评估所提出的方法4层互联架构。该表报告了e的平均值5次以上的估值精度和标准差

　　在表1中，我们报告了MNIST案例超过5次评估运行的评估准确性。我们首先观察到量化感知训练(列3-4)对模型的性能至关重要。更具体地说，在光子正弦结构中应用训练后量化方法(列2)会导致模型的性能崩溃。即使在训练后量化获得兼容性能的光子s形的情况下，它仍然会导致巨大的性能下降，特别是在分辨率低于4位的情况下。这突出了这种训练后量化方法的局限性，即在不考虑可能的异常值的情况下对参数进行统一量化，使其特别容易受到量化噪声的影响和不稳定。这种不稳定性可以通过使用量化感知的训练方法来避免，这种方法使模型对使用EMA计算代理最小值和最大值的离群值更加健壮。量化感知训练模型(列3)即使在分辨率低至3位的情况下也能显著抵抗性能下降，在这种情况下，针对完全精度模型发生的性能下降低于光子正弦和s型情况。所提出的方法(列4)在所有评估的分辨率下都取得了更好的性能，显著提高了较低比特分辨率下的精度，例如在光子正弦配置中的2比特情况下，与量化感知训练相比，精度提高了大约，突出了以混合精度方式逐渐降低比特分辨率的贡献。此外，它允许我们将两个激活函数中的位分辨率降低到3位，与全精度模型相比，最小性能降低了2位。

　　图7

　　

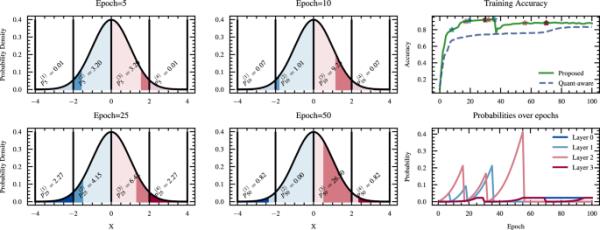
　　图描述了使用所提出方法的训练过程。前两列描述了模型在不同时期的降位概率密度分布。在最后一列的第一行中，报告了与量化感知训练相比，所提出方法的训练精度。第二行的最后一个子图描述了训练过程中每一层的概率

　　在图7中，我们绘制了每层在不同时期的概率分布，以及训练过程中的准确性，这与量化感知训练相反，让我们进一步了解所提出方法的进展。更具体地说，在图的前两列中，我们粗略地表示了网络每层在4个不同时期(5,10,25和50)的概率密度。使用该方法的默认超参数对网络进行100次训练，初始和最小分辨率分别设置为8位和2位。如图的前两列所示，中间层(第2层和第3层)在历元5中降低其位分辨率的可能性更高。在epoch 10，第二层的概率减少了，因为在epoch 5和epoch 10之间执行了位减少，而第三层的概率增加了。

　　这在图中第二行第三列的子图中得到了更清晰的描述，其中绘制了训练过程中每一层的概率。如图所示，对于每一层，概率增加，直到发生比特减少的点，每个层的这个点不同，这取决于它的位置和执行最后一次比特减少的历元。例如，对于第二层，在epoch 25之前发生了两次比特减少，一次在epoch 8，另一次在epoch 19，而对于第三层，在epoch 17只发生了一次比特减少。第三层在epoch 70(执行最后一个比特缩减)达到最大概率，之后它的概率降低到零，因为该层达到了最低可用比特分辨率(2比特)。

　　在第一行的最后一个子图中，用星号标记和层的参考颜色报告比特减少的时间。在这个子图中，我们还观察到与量化感知训练相比，所提出的方法的优点。量化感知训练在非常早期的训练阶段达到一个平台，之后只观察到微小的改进。另一方面，该方法收敛到最优局部最小值的速度更快，虽然比特减少会影响训练后期的性能，但仍然比量化感知训练的性能更好。训练结束时，采用该方法训练的模型中间层分辨率为2位，第一层分辨率为6位，最后一层分辨率为4位，比采用量化感知训练训练的模型准确率更高。

　　表2 e使用ResNet8在CIFAR10数据集上对所提出的方法进行评估。该表报告了e的平均值5次以上的估值精度和标准差

　　当我们应用所提出的渐进式混合精度量化感知训练时，在卷积架构中也获得了性能改进，如表2所示，突出了该方法的泛化能力。更具体地说，在卷积架构中，使用的训练后量化基线(列2)即使从7位分辨率也会崩溃。为此，当应用较低的位分辨率时，量化感知训练(列3)本质上有助于提高模型性能。更具体地说，通过应用量化感知训练，我们能够将位分辨率降低到4位，而性能下降更低。最重要的是，所提出的方法(第4列)使我们能够降低位分辨率，实现更好的性能。有趣的是，在光子s形的情况下，对量化感知训练的评估精度的改进比所有不同的比特分辨率都要大。

　　该方法还可以提高PNN的推理时间。使用第2节中给出的公式，我们计算不同评估运行的推理时间。更具体地说，在图8中，报告了量化感知训练和提出的方法的推理时间。如图所示，与量化感知训练相比，应用所提出的量化方法，我们能够更快、更准确地执行推理。在需要高频响应的高速率应用程序中，更快的推断可能非常有用。如前所述，无论应用何种激活函数，应用所提出的方法都可以在mlp和cnn中获得更好的平均比特精度，并在相同或更好的精度下显着减少推理时间。这突出了该方法在不同体系结构下的有效性和鲁棒性，以及它的泛化能力。

　　图8

　　

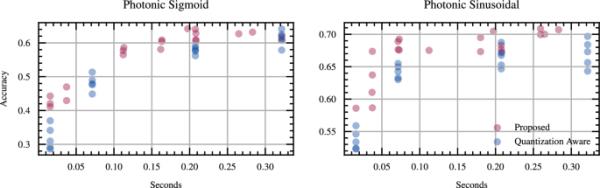
　　提出了基于精度的量化感知训练的推理次数，并提出了同时应用光子激活函数的方法

　　用于评估光子循环架构的数据集是高频金融时间序列限价订单簿数据集(FI-2020)[64]，由来自5家芬兰公司的400多万份限价订单组成。数据处理模式和评估过程在[58]中有广泛的描述。在接下来的实验中，使用了1到5的数据集分割。预测任务是预测未来中间价格在接下来的10个时间步之后的运动，它可以下降，上升或保持不变。实验中使用的深度学习网络由一个包含32个神经元的循环光子层组成，如第2节所述。循环层的输出被馈送到两个完全连接的层，分别由512和3个神经元组成。提供给模型的时间序列的长度为10(当前和过去9个时间步)。使用RMSProp优化器对模型进行了10个epoch的优化，而学习率设置为。

　　表3 e在FI2010数据集上使用RNN对所提出的方法进行评估。该表报告了在3个月的五个分裂的平均科恩卡帕度量和标准偏差估值运行

　　表3报告了两个激活函数在3次评估运行中5次分裂的平均和方差Cohen kappa分数。由于数据集高度不平衡，因此使用kappa度量。与图像分类情况类似，该方法优于基线方法，并在应用较低比特分辨率时显著提高了模型的性能。在这两个激活函数中，我们甚至可以观察到，当我们采用所提出的方法时，与完全精确的模型相比，性能有所提高。这是一种预期的行为，因为量化使网络正则化，这样就避免了过度拟合。为此，与完全精确的模型相比，在平均情况下观察到更高的分数，即使应用所提出的方法导致平均位分辨率接近4位。最后，正如所进行的实验所证明的那样，使用所提出的框架可以在广泛的应用程序、体系结构和所采用的光子配置中以较低的比特要求平均情况下获得更高的性能。

　　我们提出了一个量化感知训练框架，该框架面向均匀混合精度量化，但也可以很容易地扩展到其他量化方案，如对数和动态方法。此外，使用理论框架评估此类量化方案的能源效率是一个有前途的研究方向，因为它解锁了在实际硬件上部署之前评估量化方法的能力。这允许人们事先估计应用的PNN的能量消耗。

　　在本文中，我们的重点是降低一个模型内的位分辨率，以提高计算率，当新的动态pnn应用。更具体地说，我们提出了一种量化感知的训练方法，基于观察到中间层能够在较低的比特分辨率下运行而不会对模型的性能产生负面影响，该方法可以显着降低层的比特分辨率。该方法利用了传统量化感知训练方法的优势，因为它考虑了网络内所需的比特分布，并根据每层的位置逐渐降低每层的分辨率。考虑到已经进行的实验，我们提出正态分布概率，定义每层比特减少的可能性，并在训练过程中逐渐增加它们。该方法的有效性在各种架构、任务和光子配置中得到了证明，与评估基线相比，该方法能够显著降低模型的平均比特分辨率，并缩短推理时间。通过这种方式，它有利于模拟计算的潜在使用，更具体地说，通过进一步提高所开发的加速器的计算速率，同时保持低能耗，可以使用神经形态光子学。

　　下载原文档：https://link.springer.com/content/pdf/10.1007/s00521-023-08848-8.pdf