TALYS核反应代码的hauser - feshach统计衰变模型已被改编,以便通过迭代去激发裂变碎片来计算提示裂变中子和\(\ γ \)射线观测值。使用GEF、HF\(^{3}\)D和SPY等几个裂变碎片生成器为TALYS提供数据库。这些数据库包含标准化的表,其中包含裂变碎片产量、平均激发能及其宽度、平均总动能,以及原始裂变碎片的电荷和质量数的函数。计算结果,包括提示粒子多重度、光谱、平均能量和独立裂变产物产率,与实验和评估数据进行了比较。这项工作首先概述了在TALYS中实施的新方法,并检查了三个重要参数对最终蒸发数据的影响。此外,还详细研究了U \(^{235}\)的中子诱导裂变随入射能量的变化规律。用GEF和HF\(^{3}\)D输入的TALYS计算结果与现有实验数据和独立GEF代码计算结果进行比较。所提出的方法有助于提高模拟裂变过程的能力。
在核裂变过程中,原始裂变碎片的提示粒子发射产生各种相关的提示裂变量。这些指标包括独立裂变生成量、裂变中子增殖、裂变中子谱(PFNS)、裂变射线增殖、裂变射线谱(PFGS)和同分异构体增殖比。这些提示裂变量的特征包含了详细了解裂变物理的有价值的信息,对许多核应用都是有益的;例如,反应堆安全延迟中子产量的评估[1],核废料管理中微量锕系元素嬗变系统的设计[2],用于诊断和治疗的放射性同位素的生产[3],以及核天体物理学的研究,特别是在r过程的裂变循环期间。
然而,对不同激发能下不同裂变系统的这些观测值进行综合建模仍然具有挑战性。此外,上述应用所需的精确裂变观测值的估计仍然依赖于经验模型。例如,在ENDF/B-VIII[8]和JENDL-4.0[9]评价中使用了裂变产率的Wahl系统学[4,5,6]和异构体比率的Madland-England模型[7]。Los Alamos (Madland-Nix) PFNS模型[10]基于物理考虑;但是,它只考虑一种碎片(所谓的最可能碎片)。
在裂变过程中,复合核发生变形,因此可能接近断裂点。在二元裂变中,原子核分裂成两个互补的裂变碎片。通常,这个过程可能会产生几百对不同的裂变碎片。在质量分裂之后,新生碎片之间的库仑斥力加速了它们,背靠背。复合核的激发能和反应的q值之和分为总动能(TKE)和总激发能(TXE)。当碎片达到完全加速时,高激发态的碎片会释放出裂变中子和裂变射线,直到它们达到亚稳态或基态。然后裂变产物经历衰变。衰变发生在富含中子的独立裂变产物中。延迟中子和延迟射线从独立的裂变产物中释放出来,成为最终稳定的或长寿命的累积裂变产物。
由于裂变过程由几种不同的物理现象组成,所以各个阶段用不同的物理学来描述。目前对提示裂变观测值的建模往往没有考虑独立裂变生成量与其他提示裂变观测值之间的相关性,这在一定程度上导致了模型计算的不一致[11]。因此,最近也在进行研究,以一致地评估提示裂变的观测值。
利用hauser - feshach统计衰变理论或不应用hauser - feshach统计衰变理论,已经开发了几个计算机程序来模拟受激裂变碎片的序次发射。这些代码要么是通过蒙特卡罗采样,如CGMF[12,13]、FREYA[14,15]、FIFRELIN[16,17,18]和GEF[19],要么是通过确定性方法,如逐点模型(PbP)[20]、确定性序列发射模型(DSE)[21]和HFD[22,23,24]。
在这项研究中,我们建议使用一个共同的,一致的,记录良好的,透明的核去激励代码来探测裂变物理中初始假设的偏差和系统误差。这些系统误差可以通过在退激励阶段微调参数来补偿。我们使用现有的裂变碎片发生器来获得中子发射前裂变碎片的质量和能量产率分布,包括微观模型[25]和现象学模型[19,22,23]。核反应模型代码TALYS[26]计算激发的裂变碎片中中子和射线的蒸发,以获得即时的裂变观测值。在Hauser-Feshbach统计衰变计算中,TALYS采用了类似于HFD模型的确定性技术[22,23],但到目前为止,计算仅限于第一次裂变,在裂变之前没有中子蒸发。
图1
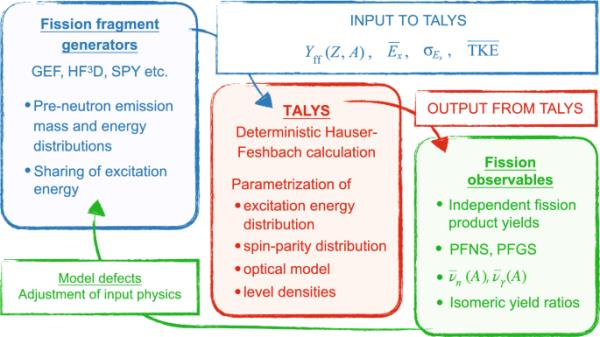
提出的工作流程,其中使用各种裂变模型为TALYS创建中子前发射数据库。TALYS的必要输入是裂变碎片产率,平均激发能,其宽度和平均总动能()。TALYS的Hauser-Feshbach形式输出的去激励数据可以与实验数据和其他独立模型代码的结果进行比较。该方法促进了全面的模型比较,解决了系统错误和模型缺陷
我们研究了铀上中子诱导裂变的详细计算,并展示了计算的中子和射线多重度、PFNS、PFGS和独立裂变产物产率,并将其与现有的实验和评估数据进行了比较。
TALYS代码(版本:1.96)包括几个计算裂变观测值的模块。TALYS中首次实现的质量产量是基于多模态随机颈断裂模型(MM-RNRM)的修订版本。最初的模型是由Brosa[27]开发的,用于计算零温度下裂变碎片的性质。在计算原子核势能格局的模型中加入了温度[28]。在变形空间中对裂变通道的搜索得到了超长(SL)、标准I (ST I)和标准II (ST II)裂变势垒和裂变前形状作为温度的函数。获得的温度相关裂变势垒和裂变前形状参数可作为TALYS中碎片质量分布计算的输入选项。然而,该模型不符合大多数实验裂变产率[29]。另一种增强中子前质量分布的方法是将GEF代码与TALYS代码直接转换为Fortran,从而结合起来。但是,此方法会锁定代码版本,并且无法顺利过渡到更新的裂变代码版本。与最近版本的GEF相比,它也可能导致很大的差异[30]。
最近实施了第三种方法[31,32],该方法利用现象学和经验代码,如GEF [19,30], HFD[22,23]和SPY[25,33]作为裂变片段生成器,为TALYS创建裂变片段数据库。使用这些数据库可以促进解决系统错误和模型缺陷的全面模型比较。图1显示了预期方法的工作流程。起始点涉及由每个碎片电荷Z和质量数A的裂变碎片产率、其高斯分布的平均激发能、激发能分布的宽度和碎片对的平均总动能()所定义的初始条件。TALYS使用这些数据库来计算蒸发数据,例如,中子和射线发射顺序,直到两个碎片放松并达到基态。在这种方法中,人们可以迭代计算来调整参数并进行敏感性研究,以揭示补偿趋势和其他相关效应[34,35]。
本节描述了用于生成裂变片段数据库作为TALYS输入的两种裂变片段生成器模型。第一个模型HFD (Hauser-Feshbach裂变碎片衰变)是一个统计衰变代码[22,23],它是通过Hauser-Feshbach统计衰变代码BeoH来研究U、U和Pu中子诱导裂变的中子和射线观测值。用确定性的方法,使它可以计算贡献包括裂变碎片具有非常低的产量,也确保异构体的产生来自一个适当的衰变方案,包括离散水平信息。在HFD模型中,裂变碎片分布是通过拟合实验数据,并根据核温度的比值(非等温模型参数)在互补裂变碎片之间分配激发能来生成的[36]。生成的裂变片段以表格形式存储在TALYS裂变片段数据库中。
第二个模型GEF[37]是一个基于蒙特卡罗的现象裂变模型,尽管采用了简单的蒸发方案,但它同时产生中子前发射量和去激发数据。本研究采用GEF (version: 2021/1.2)计算初生裂变碎片的质量和电荷产额及相应能量[30]。蒙特卡罗采样是基于每一个反应的100万个裂变事件。列表模式数据特性被激活,以允许每个裂变模拟的逐个事件输出。总共计算了737个裂变核的数据文件,范围从Os到Mc,激发能范围从0到20 MeV。生成的裂变片段以表格形式存储在TALYS裂变片段数据库中。数据被修改为只包括第一次裂变。在未来,TALYS将负责分配多机会裂变概率,从而允许在第一次裂变文件之间进行插值。
TALYS通过在所有裂变碎片的分布上集成Hauser-Feshbach统计衰变计算来计算裂变碎片的去激发,而不是蒙特卡罗采样。确定性处理的主要优点是它可以考虑到裂变事件的小概率。参考文献中解释了一种技术。(22、23、24)。
图2显示了激发裂变碎片(Z, a)的多中子和射线发射过程的示意图。初始碎片(Z, a)处于连续激发态,通过发射中子衰变为连续或离散状态,通过发射射线衰变为(Z, a)的连续或离散状态。这个连续的过程一直持续到每个状态达到基态或同分异构体状态。
图2
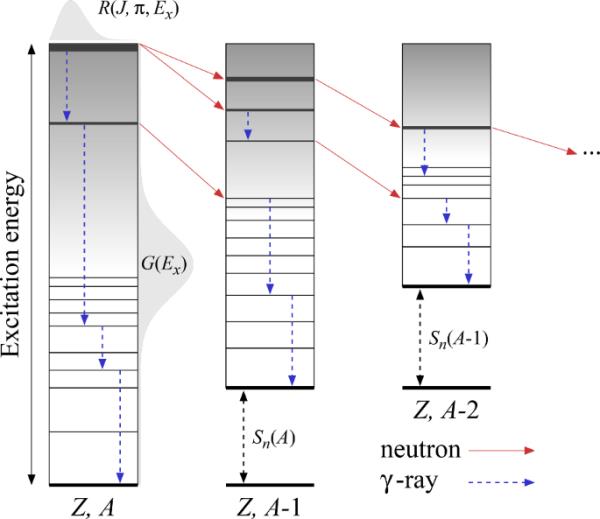
裂变碎片多中子和射线发射过程示意图(Z, a)。纵轴表示激发能,为中子分离能。实线箭头表示中子发射,虚线垂直箭头表示射线发射
为了计算这样一个去激发过程,需要原始裂变碎片的数量。TALYS从上述裂变碎片数据库中读取这些初始分布,并建立激发能分布和自旋宇称分布。给定裂变碎片的初始居群表示为:
(1)
TALYS假设激励能为高斯碎片分布,具有平均激励能和宽度,
(2)
角动量的产生仍然是当代裂变建模的一个挑战[38,39,40,41,42]。TALYS采用自旋宇称分布,遵循能级密度公式的泛函依赖[43]。由于奇偶性分布为1/2,因此假设自旋奇偶性分布表示为
(3)
为了保证与实验数据的合理吻合,引入了一个比例因子。这个新的标度参数控制了原始裂变碎片角动量的分布。
另一个重要参数是进入能级密度模型的自旋截止参数[44,45],定义为
(4)
式中为配对能量修正量,为渐近能级密度参数,a为能级密度参数。TALYS采用了另一种比例因子,表示核自旋截止参数的全局调整因子,适用于能级密度模型。这个参数乘以并影响所有独立的裂变产物,这些产物是由激发中子的发射填充的。分布和应满足归一化条件,即和。
Hauser-Feshbach模型计算中的其他成分包括中子和带电粒子的光学模型势、能级密度参数、射线强度函数和所有残余核的离散能级性质。在本研究中,我们使用了中子的konin - delaroche全局光势[46],一个复合能级密度公式(Gilbert和Cameron模型[47]),该公式使用了参考文献[48]中的能级密度参数和系统,IAEA-CRP SMLO 2019表和IAEA GSF CRP 2018用于E1和M1射线强度函数[49,50,51],以及来自RIPL-3[52]的离散能级数据。
统计hauser - feshach计算是从裂变碎片(Z, a)的初始条件进行的,而发射的中子和射线的结果是和。然后使用初始裂变产率对这些结果进行加权,以计算最终的可观测值。
给定裂变碎片的瞬间裂变中子数是通过加上初始种群产生的裂变中子数来计算的。
(5)
式中为中子多重度,为质心系统(CMS)中的中子动能谱。片段(Z, A)产生的能量为
(6)
在实验室框架中,碎片的裂变中子谱由质心系统根据Feather公式[53,54,55]转换而来:
(7)
其中是裂变碎片每核子的动能。PFNS通常用与麦克斯韦谱的比值来表示:
(8)
在这项工作中,我们采用MeV与实验和评估数据进行比较。
射线观测值可以用与中子观测值类似的方法得到。利用质心系统的初始居布数和射线谱计算了瞬发裂变射线多重度:
(9)
片段(Z, A)产生的能量为
(10)
由于中子的激发发射,原始裂变碎片产率的镜像对称性被打破,特征峰出现。独立裂变产物产率Y(Z, A)由主裂变碎片产率推导得出:
(11)
式中为主碎片(Z, A)发射中子的概率。
摘要
1 介绍
2 TALYS中的裂变模型
3.裂变碎片去激发的确定性方法
4 结果与讨论
5 结论
数据可用性声明
参考文献
致谢
作者信息
搜索
导航
#####
我们确定了控制裂变碎片统计衰变计算所必需的几个关键输入参数。为了评价裂变碎片去激发的观测值,对自旋宇称分布和连续态数进行了灵敏度研究。式(3)中的比例因子调节角动量分布。另一个比例因子通过乘法因子调整自旋截止参数。离散连续态的能量宽度由式给出
(12)
式中,N为连续态数,为最大激发能,为最后一个离散能级的激发能。在TALYS中,N随发射的核子数而变化。如果发射的核子数小于4,则N的值保持与输入值相同。但是,如果发射的核子数小于8,则修正后的连续状态数可以表示为:,其中x为发射的核子数。如果发射的核子数大于8,则值减小到N初始值的一半。
以下4.4.1对自旋截止参数的敏感性
在我们之前的研究[22]中,HFD模型表明,有必要再现高达5 MeV入射能量的中子诱导U裂变中的中子观测值。基于同一研究[22]的粗略估计,我们选择设置为4-6的范围。此外,最近的另一项研究[56]表明,对于再现中子捕获和其他反应实验中观察到的同分异构体产率,设置在0.4-0.5范围内是最佳的。
图3
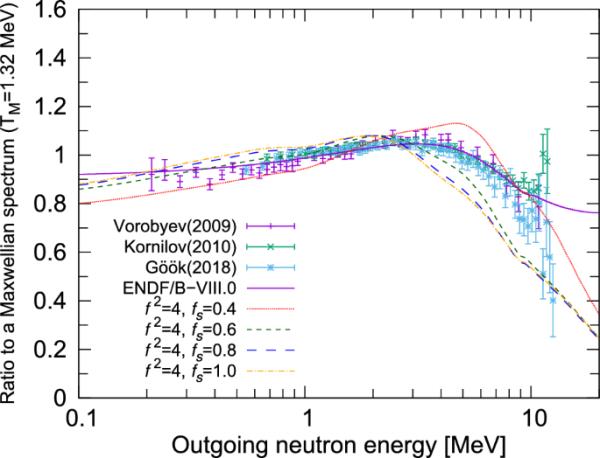
MeV下PFNS自旋截止参数与麦克斯韦光谱比值的灵敏度。反应为U(n,f),输入数据来自HFD模型
我们通过改变参数在3和6之间(单位步长变化)和参数在0.4和1.0之间(步长变化0.2)进行敏感性分析。TALYS计算的输入基于HFD获得的数据。表1给出了、、和的计算值摘要。得到的结果产率较好,但较小。结果表明,随和值的增大,两者均有明显的减小趋势。也随着增加而减少。图3显示了计算得到的PFNS与麦克斯韦谱的比值。值对2 MeV以上PFNS的峰值位置和形状均有显著影响。我们的首要任务是精确地再现中子观测值,尤其是。因此,最佳自旋截止参数为和(见表1)。
表1 prom的灵敏度pt中子和射线多重度(分别为和)和平均能量(分别为和)与U(n,f)反应自旋截止参数的变化有关。是在实验室里给出的在质心系统(CMS)中给出。
表2 prom的灵敏度中子和射线的多重度(分别为和)和平均能量(分别为和)的变化NU(n,f)反应。是在实验室里给出的在质心系统(CMS)中给出。
4.1.2 对co数量的敏感性ntinuum州
HFD模型对原始裂变碎片和衰变核均采用100 keV的恒定尺寸,而TALYS则将激发能划分为指定的N数。为了确保最大尺寸为500 keV,我们将N范围设置为50至300之间。对于-射线观测物,两者和快速裂变射线谱(PFGS)乘以对N的敏感性都表现出对N的敏感性。从表2可以看出,N值越高,发射的-射线越多。更宽的自旋分布也增加了裂变碎片的平均自旋。具有高角动量的裂变碎片不能直接达到低激发能级,因为-射线跃迁通常由偶极子跃迁控制。因此,较大的初始自旋值导致发射射线的数量增加。这与中子发射形成对比,突出了两种类型的发射之间的显著差异。随着N的增加,它也会变大因为连续态的数量也会增加。TALYS顺序地给予残核相同数量的仓作为输入,因此,随着中子的发射,仓的大小变得更小。如图4a所示,(b)为不同n数的PFGS。由此可见,PFGS中0.2 MeV以下的突出峰主要是由连续态数效应引起的。我们已经验证了箱子参数对中子观测值的影响是可以忽略不计的,因此我们选择提高与实验和评估数据的一致性。对于独立的裂变产物产率,我们已经证实这些参数的影响是足够微不足道的。
图4
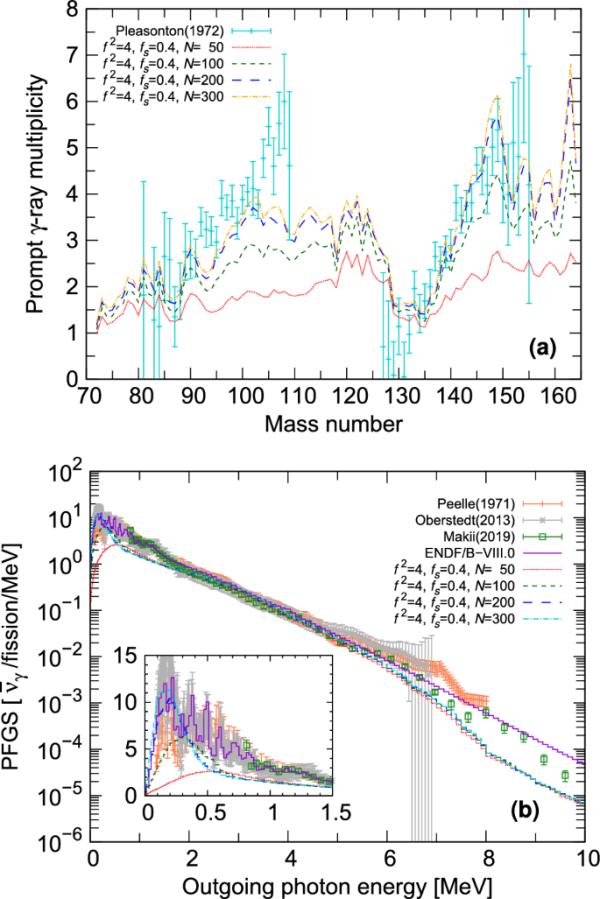
第一次中子发射后碎片N对a与质量相关的射线多重度和b PFGS乘以射线多重度的灵敏度。两种计算都是U(n,f)反应,输入数据来自HFD模型。较低能量区域的放大视图显示在b的插图中
因此,我们确定了由、和组成的输入参数集,作为获得准确的瞬发中子多重性和更好的热能射线观测值的最佳选择。
在本节中,我们比较了TALYS计算的裂变观测值与U(n,f)的实验和评估数据,入射能量范围从热到5 MeV。对两组输入数据进行计算,分别为:
1.
采用来自HFD的裂变碎片分布的TALYS Hauser-Feshbach统计衰变(以下表示为TALYS(HFD));
2.
利用GEF的裂变碎片分布(以下表示为TALYS(GEF))进行Hauser-Feshbach统计衰变。
还绘制了独立GEF代码的结果,它们被表示为GEF。TALYS(GEF)和独立GEF之间的比较突出了退激过程中的重要差异,并可能揭示有价值的模型差异,因为使用了完全相同的输入前中子数据。
4.2.1 毕业舞会Pt中子观测值
图5a为热中子能量。TALYS(GEF)、TALYS(HFD)和GEF计算结果均显示出与实验数据一致的锯齿形。在最可能的质量周围,TALYS(HFD)与实验数据相当吻合。然而,对于极不对称的质量分裂,观察到更大的差异。然而,与TALYS(HFD)和文献数据相比,在TALYS(GEF)和GEF的情况下,可以看到对重碎片的明显高估和对轻质量区域的低估。在双重魔力周围,呈现出明显的最小值。最近的实验发现表明了向更轻质量的显著转变[58]。
表3显示了计算中子和射线的平均能量的摘要,分别表示为和,分别来自TALYS(GEF), TALYS(HFD)和GEF,以及用于比较的实验和评估数据。来自TALYS(GEF)的比来自GEF的低,因为在较宽的质量范围内较低。将TALYS(GEF)和GEF与实验数据进行比较,结果表明TALYS(GEF)在轻片段中估计过低,在重片段中估计过高。这些偏差相互抵消,因此,两者都很好地符合评估数据。因为,两个TALYS结果与评估值一致。
在0.5和5.55 MeV入射能量下,U(n,f)的谱图如图5b所示。与热数据相比,TALYS(GEF)的结果与文献[59]在0.5和5.55 MeV下的实验数据更吻合。这可能是由于这些裂变数据在微调GEF激发能量共享方面发挥了重要作用。GEF中的能量分选机制[37]是重破片产生较高平均中子多重率的原因。根据m
ller等[59]的测量,增加的激发能主要在重碎片之间共享,导致来自重碎片的增加。由于TALYS(GEF)直接使用GEF的激发能,它再现了这种效应,在重碎片质量区域观察到显着增加。相反,从TALYS(HFD)获得的结果没有显示出这种观察到的趋势。这一差异归因于HFD模型中的能量排序被调整以再现[22,23]的能量依赖性。TALYS反映了GEF和HFD模型在能量分选机制上的差异。
图6表示入射中子能量从热到5 MeV的函数。计算结果表明,随着入射能量的增加,发射的中子数增加,这与已知数据一致。TALYS(HFD)成功地再现了在热能下的评估值。另一方面,TALYS(GEF)在热能下低估了约0.1的评估数据,但随着入射能量的增加,它与数据一致。
图5
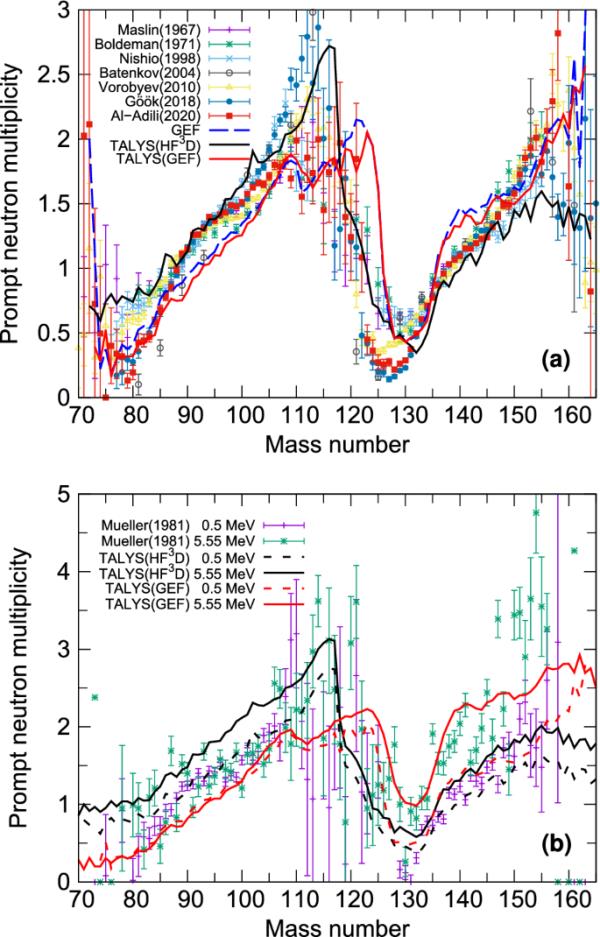
入射能量为0.5 MeV和5.55 MeV时U(n,f)反应a和b中与质量相关的中子多重率[59]
表3舞会的多重性和,中子和射线的平均能量,以及U(n,f)反应。是在实验室里给出的在质心系统(CMS)中给出。
计算得到的PFNS与MeV下麦克斯韦谱的比值如图7所示。TALYS(GEF)和TALYS(HFD)的PFNS结果都没有描述出2 MeV以上出射能量的实验数据的形状,TALYS(HFD)的尾较硬,TALYS(GEF)的尾较软。此外,TALYS(GEF)和GEF的计算结果存在较大差异,这反映了两种规范在蒸发方案上的差异。
4.2.2 毕业舞会可观测的铂射线
不幸的是,关于发射射线数量的实验数据仍然很少。然而,近年来,由于仪器和新型探测器系统的发展,测量的准确性得到了提高[60]。因此,最近的研究[64]揭示了更多的锯齿形。
本文计算的质量相关射线多重度显示TALYS(GEF)和GEF之间存在一些显著差异,如图8a所示。虽然GEF作为碎片质量的函数更平坦,但TALYS结果显示出更明显的锯齿形。结果与实验数据相当一致,尽管在碎片质量数为110附近观察到较小的射线多重度。其他当代裂变代码,如FIFRELIN[65]、PbP和DSE[66],也在几个裂变系统中验证了锯齿形。
另一个重要的裂变观测结果是释放的射线总数随入射中子能量的变化,如图8b所示。较高的激发能导致类似于在提示裂变中子中观察到的趋势的增加。TALYS大体上同意全球环境基金和评估的数据文件。目前的评估数据显示较高,因为它是基于当前的实验和理论基础数据。考虑到这些因素,TALYS倾向于低估。这种低估尚未被完全理解,但可能是由非最佳自旋截止参数引起的,已知该参数会强烈影响发射射线的数量。另一种可能的解释是,较早的实验数据表明,发射的射线总数较低,约为6.5射线/裂变,如表3所示。相反,这个值随着时间的推移而增加,最近的实验研究表明,这个数字高达8.2射线/裂变。旧的数据可能仍然用于激发能和自旋分布的微调,这可能会影响当前的计算。
另一个方面是射线的能谱。图9显示了计算的PFGS乘以与实验和评估数据的比较。TALYS(HFD)和TALYS(GEF)结果均在0.2 MeV左右观察到明显的峰值。这个峰值是由于在第4.1.2节中提到的TALYS中箱的处理。因此,与其他数据相比,TALYS结果中发射射线的平均能量往往较低,如表3所示。
图6
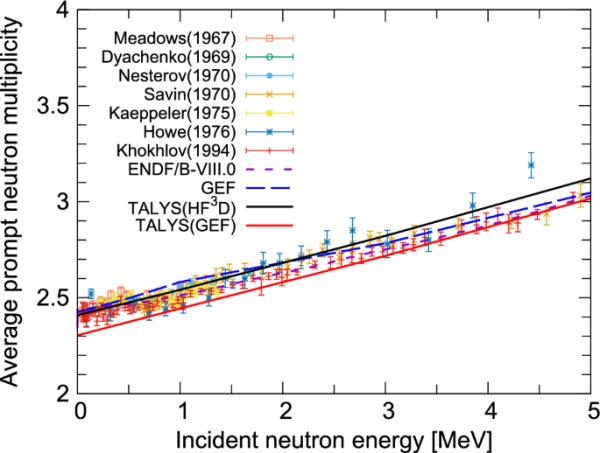
作为U(n,f)反应中入射能量的函数
图7
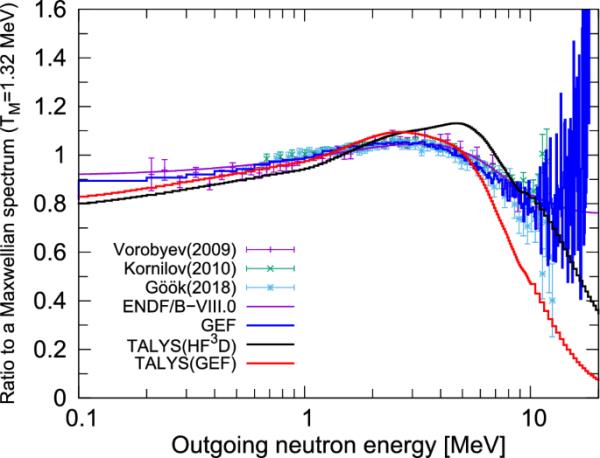
在MeV下U(n,f)反应的PFNS与麦克斯韦光谱之比
图8
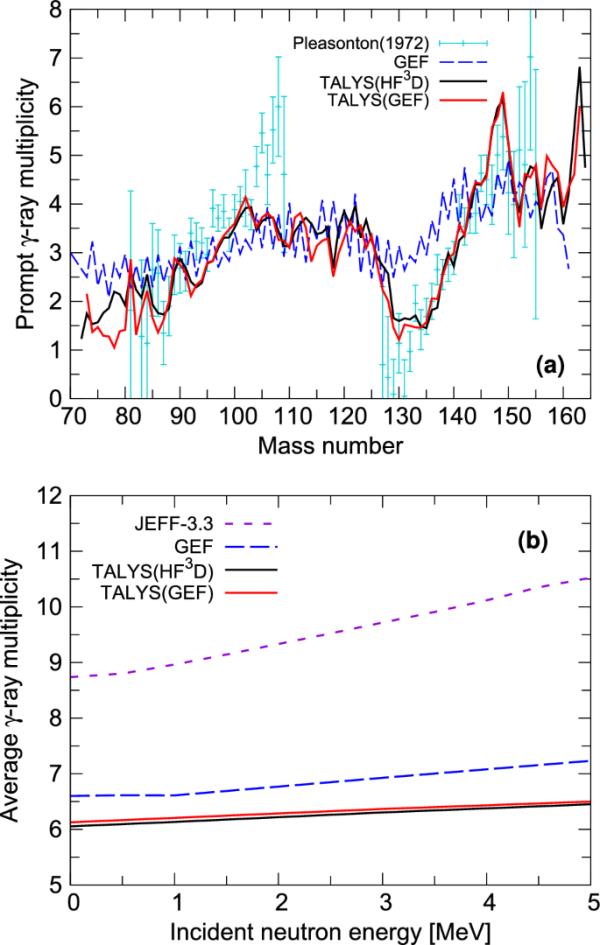
a表示U上热中子诱导裂变,b表示U上中子诱导裂变入射能量的函数
图9
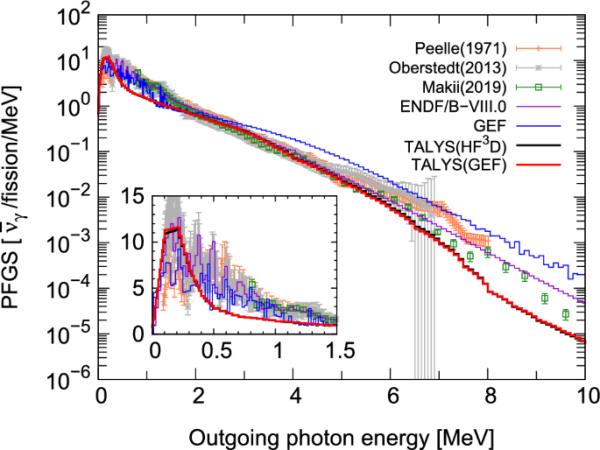
在U(n,f)反应中PFGS乘以,插图为其在1.5 MeV以下的放大图
4.2.3 独立裂变产物产率
图10显示了计算出的独立裂变生成量作为U(n,f)质量Y(a)的函数。结果表明,TALYS(GEF)和独立GEF之间的一致性,这可能导致TALYS和独立GEF对中子发射的处理类似,而中子发射与中子分离能密切相关。两种结果都重现了裂变产物产量的显著峰值,例如重碎片的峰值和轻碎片的峰值。在TALYS(GEF)中再现了峰值,而TALYS(HFD)没有再现峰值,而原始HFD模型再现了峰值[22]。
图10
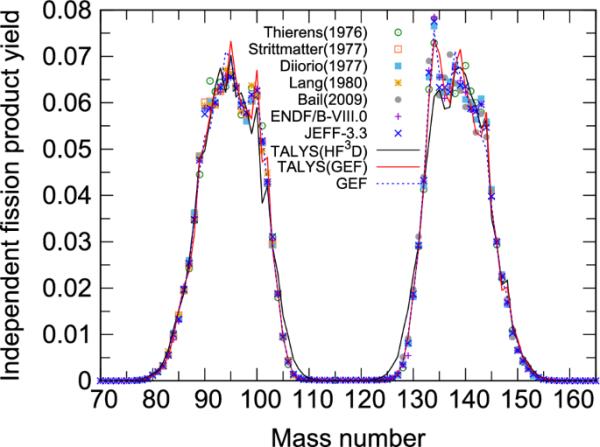
独立裂变产物U(n,f)
将计算得到的几种裂变产物的Y(Z, A)与Rudstam等[67]的实验数据进行对比,如图11所示。TALYS(GEF)和TALYS(HFD)结果与实验数据吻合良好,产率在0.001以上时,计算/实验(C/E)比接近1.0。然而,Y(Z, A)在约0.001以下的C/E中有更大的分散。TALYS(GEF)和TALYS(HFD)的结果与实验数据显示的趋势大致一致,实验不确定性也很大。
图11
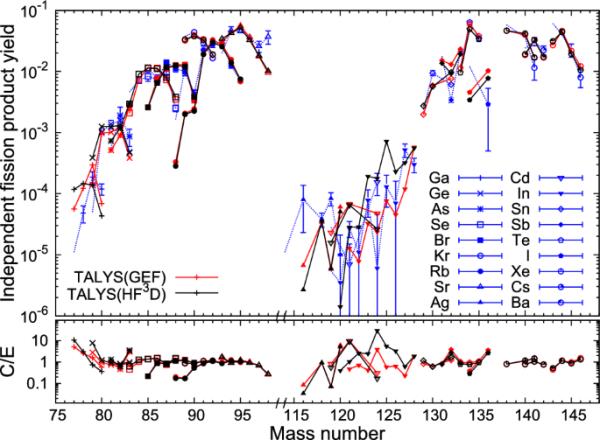
计算得到的独立裂变生成量Y(Z, A)与Rudstam等[67]在U(n,f)中的实验数据的比较
提出了一种计算核裂变数据的新方法。这个过程包括使用裂变代码为TALYS的Hauser-Feshbach形式提供输入。为了说明这种方法,使用两个裂变代码GEF和HFD来创建数据库,这些数据库随后用作TALYS的输入。TALYS结果与实验/评估数据和独立GEF代码的结果进行了比较。由于实现了包含裂变碎片产量及其激发能分布信息的标准化格式,这样一个数据库的开发简化了来自其他代码开发人员的裂变数据。采用这种新的标准格式鼓励裂变模型开发人员准备并向TALYS提供输入数据。
在入射能量从热到5兆电子伏特的情况下,选择中子诱导的铀裂变来验证这一过程。我们主要研究了裂变观测值对三个参数的敏感性,即连续态数(N)、能级密度公式中自旋截止参数的标度因子()和原始裂变碎片角动量占比因子()。我们选择和是因为它们与中子观测值很吻合。此外,我们选择了特别精细的平均总射线多重性。
在调查过程中,TALYS显示了与提示中子观测实验数据的良好一致性,例如,提示中子的锯齿形和总平均数量作为入射能量的函数。然而,在TALYS(GEF)和TALYS(HFD)结果之间观察到显著差异,再次突出了裂变中能量分配的不同物理考虑和假设的重要性。TALYS(GEF)和TALYS(HFD)的提示中子谱结果都没有描述实验数据所显示的形状,这表明需要进一步的研究和模型调整。
对于瞬发射线观测,TALYS的结果倾向于呈现锯齿状,这与最近的实验结果一致。尽管如此,在绝对规模上还是被低估了。总瞬发裂变射线谱(PFGS)在0.2 MeV左右出现一个强峰值,这被认为是TALYS编码中的一种起始效应,它低估了某些区域(如低于2 MeV和高于6 MeV)的实验数据。
TALYS(GEF)的独立裂变产物产率Y(A)与实验数据和最近的评价总体上吻合良好,再现了独立裂变产物产率结构中明显的峰值(at)和低谷。对于Y(Z, A),两种TALYS结果与文献数据基本一致。
在未来,更多的相关物理量将被研究,如累积裂变产物产率,射线观测值和同分异构体产率比。早先已经使用TALYS来计算基于不同假设的新生裂变碎片角动量产生的同分异构体产率[68,69,70,71]。然而,这些计算侧重于单个同分异构体产率,并利用外部自旋能矩阵实现。此外,没有特别强调其他裂变观测。这项工作的前景是利用内环的新实现来产生系统的全局同分异构体产率研究,作为质量和激发能的函数,考虑到不同裂变观测值之间的相关性。
下载原文档:https://link.springer.com/content/pdf/10.1140/epjas10050-023-01095-4.pdf



