湍流壁面流动中动量和传热的精确计算建模仍然是一项具有挑战性的任务，特别是对于具有高分子普朗特数的流体。由于温度梯度较大，流体性质的剧烈变化成为另一个重要问题。目前的直接数值模拟研究专门解决了这一问题，考虑了具有温度依赖材料特性的真实传热油的代表性工作流体。在受热壁面附近，尽管焓波动明显增加，但分子粘度的增加显著减弱了动量和热量的湍流对流通量。由于导热系数随温度的下降明显小于粘度的下降，因此阻尼的湍流混合显著降低了努塞尔数，而表面摩擦系数与流体性质恒定的情况仅略有不同。径向速度波动的衰减持续降低了湍流动量和热通量预算中的产生项，而焓波动的产生只是从壁面移开，峰值水平没有显著变化。湍流轴向应力预算中的再分布也减弱了，减少了基于压力-应变的湍流向各向同性的转向。因此，面对更加各向异性的湍流运动，对主要为各向同性湍流建立的标准湍流模型提出了进一步的困难。

　　高普朗特数液体最常用于各种工业工程应用的润滑和冷却。最小湍流动力尺度和热尺度的巨大差异对动量和热量输运的计算建模提出了强烈的挑战。随着分子普朗特数的增加，近壁层的热阻增大，使得与换热有关的基本热物理现象向壁面附近移动。与之相关的较陡的温度梯度通常会导致流体性质的显著变化。通常认为忽略这种变化可能会大大增加预测的不确定性。

　　为了对具有显著材料特性变化的动量和能量传递进行可靠的描述和最终充分的计算建模，有必要详细了解近壁层中潜在的输运过程。直接数值模拟(DNS)的计算方法基本上可以提供所需的高度准确和全面的洞察力，根据定义，它试图在数值上捕获近壁层中发生的所有相关的动态和热小尺度结构。

　　在非加热等温条件下，对于完全发育的通道流和管道流，已有非常丰富的文献。其中，我们举例提到Wu和Moin (2008)， Boersma(2011)的研究，他们对非加热管道流动进行了高分辨率的DNS，详细分析了一阶和二阶湍流力矩。对于传热的DNS，大多数人认为低分子普朗特数，以单位为代表气体，以及恒定的材料性质，如Kim和Moin (1987)， Piller (2005)， Kawamura等人(1998)，Redjem-Saad等人(2007)的工作。考虑到与液体更相关的条件，Na和Hanratty (2000)， Kozuka等人(2009)研究了分子普朗特数高达的湍流通道流动的高阶湍流统计量。Tiselj等人(2001)的DNS在考虑固体壁面的共轭传热时考虑了平面通道流动。Schwertfirm和Manhart(2007)提出了与高普朗特数下的传热模拟相当的DNS模拟，在非常高的施密特数下，湍流通道中的被动标量输移达到。

　　迄今为止，相对较少的普朗特数超过单位的DNS考虑了与温度相关的材料性质，这是本工作的重点。在这些先前的研究中，Lee等人(2013)通过在普朗特数下对具有温度依赖粘度的湍流边界层进行DNS，研究了壁面加热对表面摩擦系数的影响。Zonta等人(2012)研究了温度依赖粘度对具有加热和冷却壁面的通道流动中强制对流的影响，特别说明了靠近通道热侧的低粘度区域的影响。应用Boussinesqu近似，用各种不可压缩DNS研究了体积膨胀引起的密度变化的影响。根据壁面密度的法向变化，浮力可以形成稳定或不稳定的分层流动条件，湍流平流输运基本上分别受到抑制或增强。García-Villalba和álamo(2011)研究了稳定分层的平面通道流动，将摩擦理查德森数增加到再层化的极限，其中内心流区域受浮力的影响最强烈，而近壁区域基本上与中性情况相似。Zonta和Soldati(2018)的综述解决了稳定分层流动通常遇到的计算和实验问题。Scagliarini等人(2015)的DNS研究了中等摩擦雷诺数下的不稳定分层通道流动，结果显示，在上面的瑞利数下，壁面法向速度波动明显增强，而在下面，浮力的影响微乎其微。Patel等人(2015)认为强可压缩流动与由热力学压力的实质性变化引起的密度高变化有关。结果表明，引入半局部标度可以有效地将变化流体性质的湍流速度统计量与相应的常数性质结果相融合。后来，Patel等人(2017)提出了一种类似的标度方法，用于普遍描述温度。Nemati等人(2016)的DNS考虑了超临界压力下的加热湍流管道流动，面临非常特殊的非单调材料性能变化。他们观察到由这些变化引起的传热显著恶化。

　　最近的大多数高分辨率DNS都集中在雷诺数增加的影响上，同时假设普朗特数不超过单位和恒定流体性质(Alcántara-ávila et al. 2021;Moser et al. 1999;Pirozzoli et al. 2022;Hoyas et al. 2022;Yao et al. 2023)。另一方面，对于通过小截面通道输送特定高普朗特数冷却剂的各种紧凑型液冷系统，其湍流雷诺数相当低。相关的低传热率始终导致较高的壁体过热，因此材料性能的温度依赖性成为一个问题。目前的DNS研究特别研究了这些条件，假设具有代表性的实际冷却剂具有分子普朗特数以上和中等雷诺数以下的条件。与温度相关的流体性质对湍流统计的影响应与恒定材料性质的相应结果进行比较分析。对于所考虑的设置，由于体积膨胀引起的密度变化始终保持足够小，因此浮力的影响可以忽略不计。在讨论结果时提出的低理查森或瑞利数字也将支持这一点。

　　目前的DNS解决了质量、动量和能量的不可压缩守恒方程的无量纲表示，表示为

　　(1) (2) (3)

　　分别以管径D、壁面摩擦速度、壁面摩擦比焓为参考标尺。表示施加的恒定平均壁热流密度。和分别表示柱面坐标系下的无量纲速度矢量和壁值的比焓差。表示应变张量的速率。标有星号的材料性能，比热，导热系数，分子粘度和密度，总是指相应的壁值。与假设的不可压缩低马赫数流动相一致，密度与压力解耦，因此由于体积膨胀，密度可能只随温度变化。和分别表示温度下基于壁面参考条件的雷诺数和普朗特数。在假定流动由恒定的平均轴向压力梯度驱动并由恒定的平均壁热流加热的情况下，术语和with源于轴向周期性的强制执行。

　　守恒方程。(1-3)在柱坐标下直接求解，在空间上采用四阶精确有限体积离散，在时间上采用二阶精确Adams-Bashforth格式。使用CFL数设置为0.5来动态调整时间步长。

　　图1显示了计算域，轴向延伸超过5个直径。规定了速度的无滑移边界条件，并在壁面处施加均匀的时间平均壁面热流。周期边界条件用于所有轴向流动和热变量，假设动态和热充分发展的流动。从严格意义上讲，后一种假设与温度相关的材料特性相冲突，其平均值可能由于壁面加热而轴向变化。然而，对于考虑的区域长度，轴向变化在数量上远远低于垂直于壁面的径向变化，因此可以合理地忽略它，证明了充分发展的流动条件和轴向周期性的假设是合理的。

　　计算网格分别由径向、方位角和流向方向的单元组成。为了捕获小尺度的近壁结构，网格在朝向实体壁和管道中心的径向上聚集，而在均匀的方位角和流向方向上使用均匀的网格间距。以墙单元测量得到的墙附近网格分辨率为、、、。

　　图1

　　

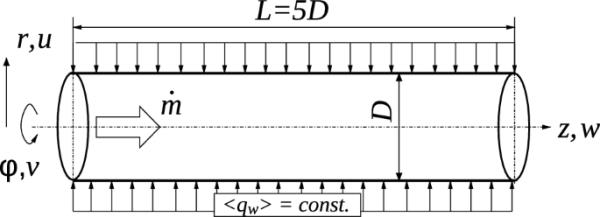
　　计算域

　　选用导热油和具有代表性的操作液，在各种技术应用中经常用作冷却剂。在考虑的温度范围内，所选油的材料特性的变化如图2所示。分子粘度的温度依赖性明显最强，而其他性质的变化则相当温和。对于所研究的热条件，目前假设的真实油提供的分子普朗特数的目标范围远远超过1，是数量级的，而最小热结构的空间分辨率要求在计算上仍然是可行的。实际预测的局部变化将在下面的结果讨论中进一步显示。

　　图2

　　

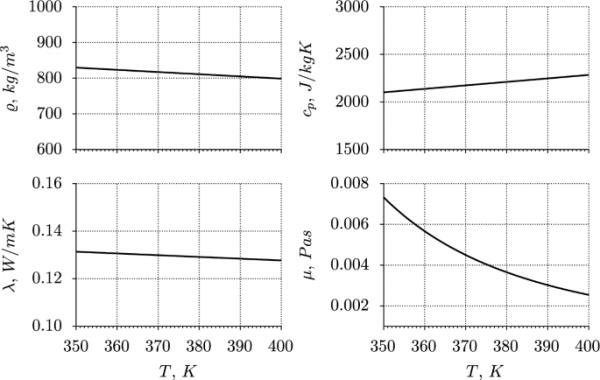
　　材料的温度特性

　　图3

　　

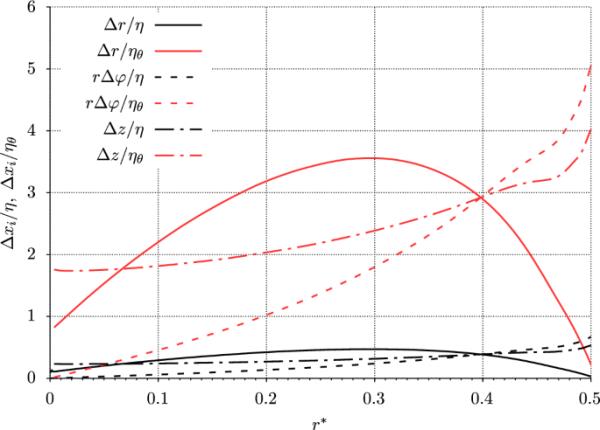
　　空间分辨率由Kolmogorov尺度和最小湍流热尺度与无量纲径向位置归一化

　　摘要

　　1 介绍

　　2 数学公式

　　3.结果

　　4 DNS验证

　　5 湍流统计

　　6 动荡的预算

　　7 结论

　　数据Availibility

　　缩写

　　参考文献

　　作者信息

　　道德声明

　　相关的内容

　　搜索

　　导航

　　#####

　　假设壁面平均温度为参考，根据壁面条件，用摩擦雷诺数和分子普朗特数来表示所研究的充分发展的管道流动。均匀施加的平均壁热流为。所选择的设置，假设管径d=12mm，产生壁面摩擦速度m/s和壁面摩擦焓J/kg，用于重新计算壁面单位。可变和恒定流体性质的结果通常分别称为“VFP”和“CFP”。

　　图3用Kolmogorov尺度和Batchelor尺度分别对动态湍流结构和最小热结构的空间分辨率质量进行了评估，其中为分子运动粘度，为湍流动能的平均耗散率。目前使用的DNS网格能较好地解析整个截面上的动力结构和热结构。此处显示的VFP情况下的径向变化在数量上非常接近或部分低于近期其他DNS研究，如Nemati等人(2016)、Zonta等人(2012)、Lee等人(2013)，其中具有最佳分辨率的研究显示了壁法向、展向和流向内的变化，与目前的分辨率相当。

　　根据文献中先前DNS的数据进行有意义的验证只能针对恒定物质属性(CFP)情况进行，因为目前考虑的特定液体和操作条件没有可比数据。由于在CFP情况下，流场和热场基本解耦，因此预测的速度的一阶和二阶统计量是根据Wu和Moin(2008)广泛使用的参考数据进行验证的，他们在几乎相同的摩擦雷诺数下对等温湍流管道流动进行了高度分辨的DNS。从图4中无因次壁面距离的变化可以看出，平均轴向速度和各个方向的速度波动的一致性很好。

　　图4

　　

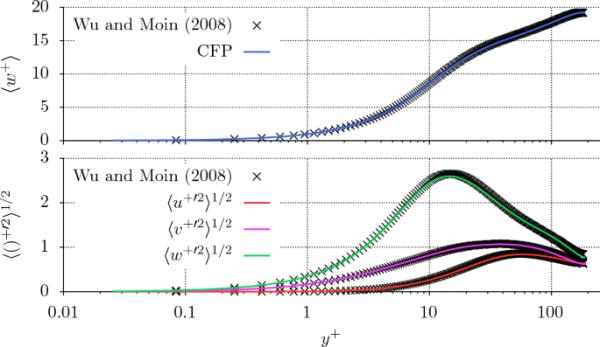
　　与文献数据比较，CFP病例的径向、方位角和轴向的平均轴向速度和速度均方根波动随壁面距离的变化

　　在非常稀缺的可用于高分子普朗特数的高保真DNS数据中，发现Schwertfirm和Manhart(2007)的DNS最符合当前的CFP条件。先前的研究考虑了在相当摩擦雷诺数下(基于通道半宽度)完全发育的平面通道，包括在高施密特数下直至规定壁通量恒定的传质方面的被动标量传递，这些都可以被认为与本CFP情况下的动量和传热条件相当。如图5所示，我们再次看到输运标量的平均值和涨落都非常吻合。Schwertfirm和Manhart(2007)普遍较低的预测概况是预期的和合理的，由于假设的施密特数和普朗特数的不平等，尽管很小。正如图3中空间分辨率的评估所示，通过文献对DNS的验证证明，目前的预测是我们分析的可靠数据库。

　　图5

　　

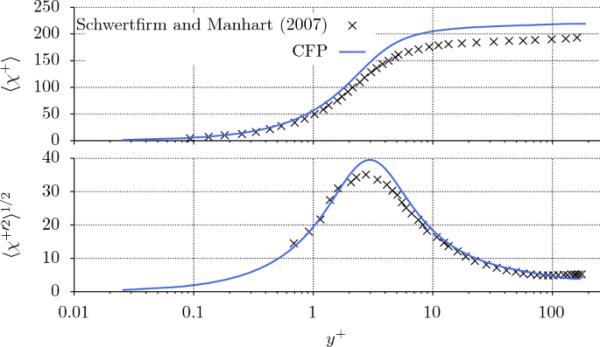
　　与文献中等效被动标量数据相比，CFP情况下的平均焓和焓均方根波动

　　对于所考虑的中等雷诺数湍流，动量和热量的湍流平流和扩散输运之间的紧密相互作用在很大程度上取决于材料性质中规定的各自的分子输运系数。因此，首先分析它们在VFP情况下的局部变化，分别讨论它们的径向平均剖面和由此导出的局部关键参数，如图6a-c所示。正如图2所示的温度依赖关系所预测的那样，动态粘度随与加热壁的距离的变化在数量上最强，而比热容、密度和导热系数的相对变化要小得多，几乎可以忽略不计。因此，局部普朗特数和局部雷诺数本质上反映了分子粘度的变化趋势，分别随着壁距的增加而显著增加/减少。由于密度变化很小，因此在后续的统计湍流分析中始终忽略其湍流波动，只考虑其在的平均值。因此，所分析的所有流量和热的波动都是基于雷诺平均，没有密度加权。非常小的密度相对变化，在最大，也转化为低摩擦理查德森和瑞利数。对于所考虑的条件，它们变成和，这证明了忽略浮力的理由。

　　图6

　　

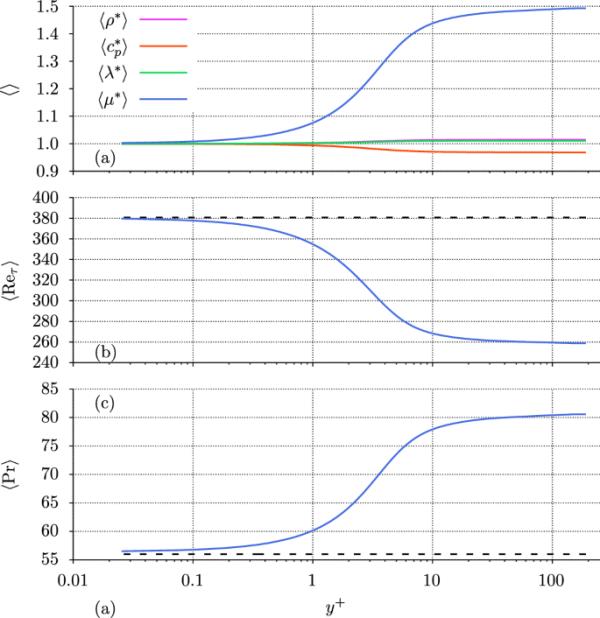
　　a平均流体性质，b雷诺数，c分子普朗特数与壁距的关系

　　黏度引起的局部雷诺数的降低导致径向和方位速度分量的湍流波动得到了广泛的抑制，而轴向分量的峰值反而增加并向中心偏移，如图7所示。与受抑制的湍流波动运动相反，热波动明显增强，这可归因于局部分子普朗特数的增加。相关的高导热电阻本质上意味着更陡峭的温度梯度，促进了VFP中更大的温度湍流波动。

　　图7

　　

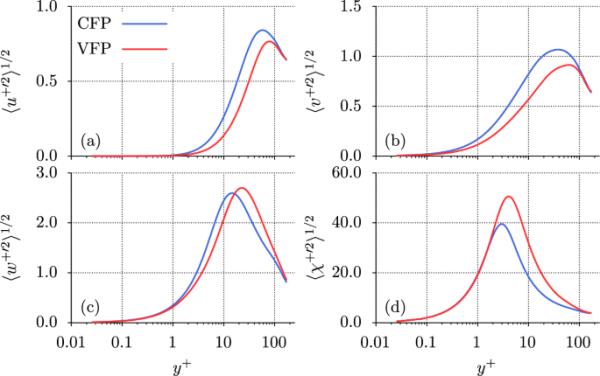
　　径向速度，b方位速度，c轴向速度和d焓相对的均方根波动

　　尽管观察到湍流速度和热波动的相反趋势，径向速度波动增加的粘性阻尼仍然在动量和热量的总通量预算中占主导地位

　　(4) (5)

　　图8

　　

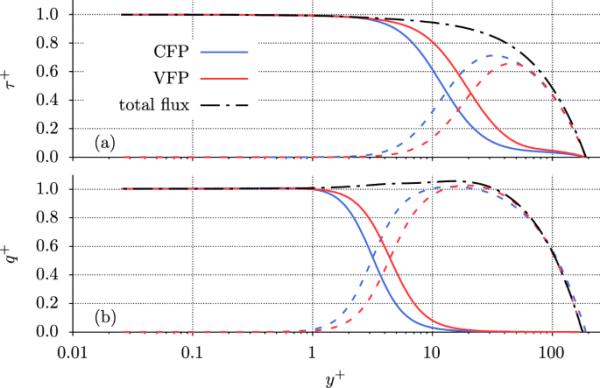
　　切应力和热流随壁距的变化:实线、虚线、虚线

　　分别。由材料性质的湍流波动引起的非线性分量对扩散通量的贡献可忽略不计，因此通常省略。

　　如图8所示，在壁面附近，湍流贡献总是减小，而层流分量反而增加。在参数意义上，因此在VFP的情况下，雷诺数效应似乎比普朗特数效应更占优势。然而，层状剪切应力的显著增加在很大程度上被同样显著增加的分子粘度所抵消，这有效地转化为壁面附近较低的剪切速率，如图9b所示。如图9a所示，与较低的近壁梯度相一致，VFP的平均轴向速度增长较慢，远低于CFP的剖面。在远离热壁区域的更远的地方，在分子粘度接近相当均匀的体积水平的地方，趋势相反，VFP剖面增加得更快，这也反映在该区域的剪切速率更大。这种补偿行为使计算得到的体速度从

　　（6）

　　彼此非常接近，从而得到的摩擦系数为

　　（7）

　　只有很小的变化，从。

　　图9

　　

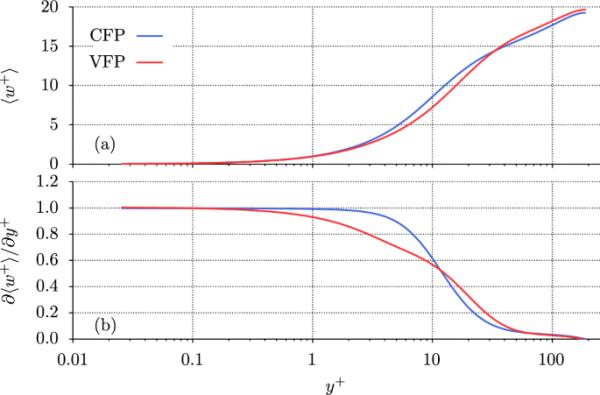
　　a平均轴向速度和b剪切速率与壁距的关系

　　与动量的粘性传递相反，图8b中层流热流分量的明显增加几乎等同地增加了焓梯度。与分子粘度不同，导热系数随温度的变化基本保持不变，因此它不会显著补偿较高的层流导电通量。因此，如图10b所示，VFP的焓梯度始终保持较高，有效地导致了整个径向域的较高剖面，如图10a所示。由此增加的壁面过热由壁面与体差表示为

　　（8）

　　最后产生一个用努塞尔数表示的强简化的全局换热系数，由

　　（9）

　　从。

　　图10

　　

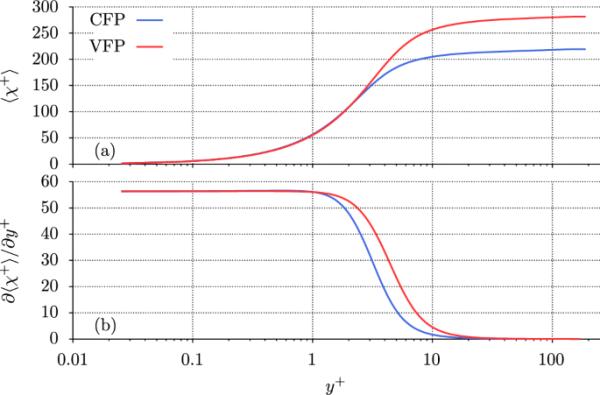
　　a平均焓差和b焓梯度随壁距的变化

　　VFP在湍流速度波动中观察到的不同趋势反映在相应的湍流预算中，通常在这里用指标符号重写为

　　（10）

　　与

　　式中，为平均对流、产生、湍流扩散、速度压力梯度张量、粘性扩散、耗散、粘性应力波动张量。将式(10)重写为法向轴向湍流应力，生产项的表达式为

　　（11)

　　如图8a和9b所示，由于湍流通量较小，剪切速率也较低，因此VFP在壁面附近的剪切速率仍然较低。因此，如图11a所示，在局部较高的剪切速率的支持下，在内部和外部开始径向增加，甚至超过了CFP值。然而，产生的能量的较小比例通过压力-速度相互作用重新分配给其他正应力分量，正如预算中出现的显著较低的重新分配项所表明的那样

　　这种较弱的再分布也解释了轴向速度波动rms上升至峰值的原因，该峰值在径向上更向内，在数量上甚至高于CFP，如图7c所示。压力应变诱导的湍流向各向同性的转向在VFP中明显减弱，从而使湍流更具有各向异性。

　　图11

　　

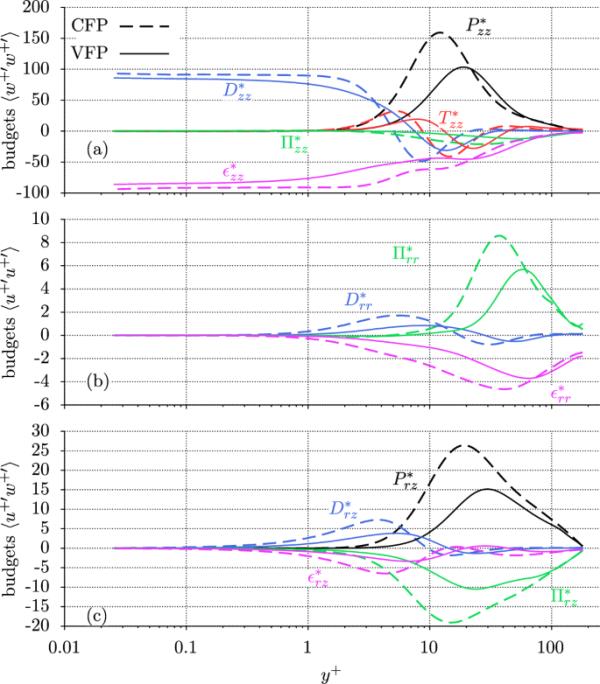
　　a、b和c的预算

　　图11b显示了径向法向应力分量的预算。基于压力-速度相互作用的再分配，在这里发生为

　　在径向区域的大部分区域，VFP明显更低。由于这个预算本身除了再分配项之外没有其他来源，因此基本上从其中获得的能量投入大大减少了。如图7a所示，在VFP的情况下，径向速度波动的强度通常保持在一个明显较低的水平，并伴随着相对较强的耗散所带来的更明显的损失。作为一个重要的结果，径向速度波动的减小显著降低了紊流剪切应力预算中的产量

　　(12)

　　如图11c所示。如图8a所示，在整个热近壁区域，VFP的明显产量下降与较低的湍流剪切应力一致。湍流剪切应力的减少反过来转化为轴向湍流应力的降低，以这种方式结束所谓的“湍流循环”。如图12所示，该示意图由与VFP情况相关的热回路扩展，最初是为了描述单个预算之间的湍流能量交换而引入的(Leschziner 2000)。

　　图12

　　

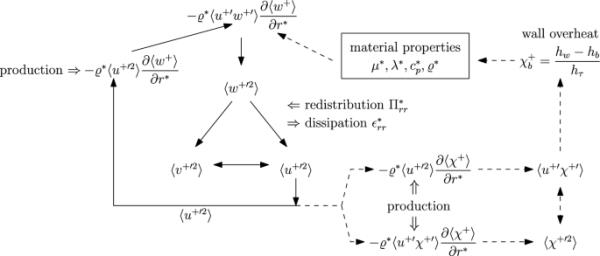
　　湍流循环，由VFP(虚线路径)的传热回路扩展

　　与速度涨落类似，热涨落和湍流热通量的预算用指数符号表示

　　(13)

　　与

　　和

　　(14)

　　与

　　分别。从图13的预算中可以看出，各自的产量为

　　(15)

　　再次从加热壁上移开，用于VFP。然而，由于持续较高的焓梯度，如图10b所示，然后上升到与CFP情况几乎相同的最大水平。再加上图6c中局部分子普朗特数的显著增加，这很容易解释图7d中VFP相对较高的峰值和增加的芯流水平。

　　图13

　　

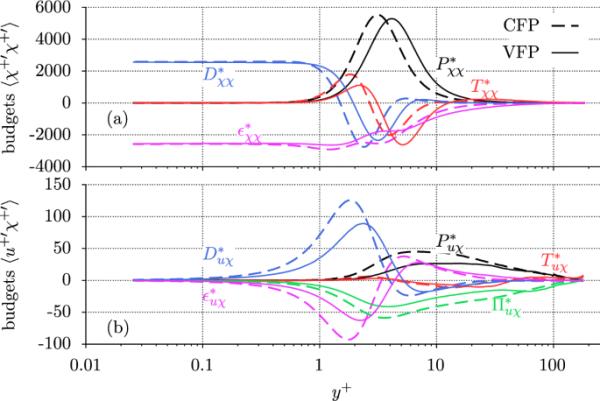
　　a和b的预算

　　与之相反，在径向湍流热通量的预算中产生，写为

　　(16）

　　通过定义更明显地反映了与VFP相关的显著衰减。因此，从图13b中可以看出，大部分都远远低于CFP情况的相应剖面，这最终导致图8b中VFP在壁面附近的径向湍流热流密度较低。因此，明显降低的传热率维持了湍流运动的潜在衰减，这在径向速度波动中最显著地观察到。由此产生的更大的壁体温差(壁过热)，如图10a所示，反过来转化为更高的分子体粘度，进一步促进了湍流速度分量的粘性阻尼。图7d中VFP的增强热波动并不能补偿壁面附近湍流径向热通量的降低，因为径向热通量在内部达到峰值。

　　图12所示的扩展湍流循环概述了湍流径向法向应力在所有涉及的近壁传递过程中的关键作用。作为最显著的特征，粘性阻尼的增加有效地减弱了湍流能量对动量和热的湍流通量的反馈，这主要是由于各自的产生项和减少，以及更高的耗散损失

　　对于所考虑的高普朗数工作流体和操作条件，分子粘度随着与加热壁距离的增加而强烈增加，最显著地调节了动量和热量的传递过程。局部雷诺数和普朗特数随温度变化的相反趋势导致速度波动，特别是径向(壁法向)分量的显著衰减，而热焓波动则强烈增强。后者的增加幅度不够大，而且径向位置偏内，无法补偿壁面附近强烈阻尼的湍流对流，导致VFP的湍流热通量和努塞尔数相当小。因此，局部雷诺数变化的影响大于局部普朗特数的影响。

　　与努塞尔数相反，VFP的表面摩擦系数几乎保持不变，这是由于分子粘度和导热系数对温度的依赖程度非常不同。分子粘度的增加在很大程度上覆盖了总剪应力预算中层流分量的增加，因为湍流分量减少了。因此，在壁面附近的速度梯度保持较低，而焓梯度随着层流热流分量的增加而几乎相等地增加，因为导热系数没有显著增加。动量和热传递的明显不同趋势强烈质疑雷诺类比的适用性，雷诺类比在标准湍流模型中被广泛假定为直接将湍流热扩散率与涡流粘度联系起来，引入了一个阶单位的湍流普朗特数。

　　径向湍流速度分量的衰减强烈地影响了所有湍流收支，持续地降低了湍流动量和热通量的产生项。在正反馈机制的意义上，较低的传热率有效地维持了粘度诱导的阻尼，因为受影响的体温降低必然导致更高的粘度。轴向湍流应力的再分布也减弱，这意味着在压力-应变相互作用的驱动下，湍流向各向同性的转向不那么强烈。因此，在径向内区域更多的各向异性湍流进一步代表了对湍流建模的进一步可能的挑战，假设主要是各向同性。

　　下载原文档：https://link.springer.com/content/pdf/10.1007/s10494-023-00474-7.pdf